John C. Baez's Blog, page 56

Random Points on a Group

In Random Points on a Sphere (Part 1), we learned an interesting fact. You can take the unit sphere in , randomly choose two points on it, and compute their distance. This gives a random variable, whose moments you can calculate.

And now the interesting part: when n = 1, 2 or 4, and seemingly in no other cases, all the even moments are integers.

These are the dimensions in which the spheres are groups. We can prove that the even moments are integers because they are differences of dimensions...

Random Points on a Sphere (Part 2)

This is the tale of a mathematical adventure. Last time our hardy band of explorers discovered that if you randomly choose two points on the unit sphere in 1-, 2- or 4-dimensional space and look at the probability distribution of their distances, then the even moments of this probability distribution are always integers. I gave a proof using some group representation theory.

On the other hand, with the help of Mathematica, Greg Egan showed that we can work out these moments for a sphere in an...

Random Points on a Sphere (Part 1)

John D. Cook, Greg Egan, Dan Piponi and I had a fun mathematical adventure on Twitter. It started when John Cook wrote a program to compute the probability distribution of distances where and were two randomly chosen unit quaternions:

• John D. Cook, How far is xy from yx on average for quaternions?, 5 July 2018.

[image error]

Three things to note before we move on:

• Click the pictures to see the source and get more information—I made none of them!

• We’ll be ‘randomly choosing’ lots of points on sphe...

Beyond Classical Bayesian Networks

In the final installment of the Applied Category Theory seminar, two students explain a category-theoretic approach to Bayesian networks and their generalizations. Check it out:

• Pablo Andres-Martinez and Sophie Raynor, Beyond Classical Bayesian networks, 7 July 2018.

Pablo Andres-Martinez is a postdoc at the University of Edinburgh, working in the cool-sounding Centre for Doctoral Training in Pervasive Parallelism. Sophie Raynor works at Hoppinger. Their blog article discusses this paper:

•...

Bayesian Networks

In the final installment of the Applied Category Theory seminar, two students explain a category-theoretic approach to Bayesian networks and their generalizations. Check it out:

• Pablo Andres-Martinez and Sophie Raynor, Bayesian networks, 7 July 2018.

Pablo Andres-Martinez is a postdoc at the University of Edinburgh, working in the cool-sounding Centre for Doctoral Training in Pervasive Parallelism. Sophie Raynor works at Hoppinger. Their blog article discusses this paper:

• Joe Henson, Raym...

Symposium on Compositional Structures

There’s a new conference series, whose acronym is pronounced “psycho”. It’s part of the new trend toward the study of “compositionality” in many branches of thought, often but not always using category theory:

• First Symposium on Compositional Structures (SYCO1), School of Computer Science, University of Birmingham, 20-21 September, 2018. Organized by Ross Duncan, Chris Heunen, Aleks Kissinger, Samuel Mimram, Simona Paoli, Mehrnoosh Sadrzadeh, Pawel Sobocinski and Jamie Vicary.

The Symposiu...

Toric Geometry in Reaction Networks

I want to figure out how to use toric geometry in chemistry. This is a good intro to toric geometry:

• William Fulton, Introduction to Toric Varieties, Princeton U. Press, 1993.

and this is a great explanation of how it shows up in chemistry:

• Mercedes Perez Millan, Alicia Dickenstein, Anne Shiu and Carsten Conradi, Chemical reaction systems with toric steady states, Bulletin of Mathematical Biology 74 (2012), 1027–1065.

You don’t need to read Fulton’s book to understand this paper! But you...

Coupling Through Emergent Conservation Laws (Part 8)

joint post with Jonathan Lorand, Blake Pollard, and Maru Sarazola

To wrap up this series, let’s look at an even more elaborate cycle of reactions featuring emergent conservation laws: the citric acid cycle. Here’s a picture of it from Stryer’s textbook Biochemistry:

I’ll warn you right now that we won’t draw any grand conclusions from this example: that’s why we left it out of our paper. Instead we’ll leave you with some questions we don’t know how to answer.

All known aerobic organisms use...

Coupling Through Emergent Conservation Laws (Part 7)

joint post with Jonathan Lorand, Blake Pollard, and Maru Sarazola

Last time we examined ATP hydrolysis as a simple example of coupling through emergent conservation laws, but the phenomenon is more general. A slightly more complicated example is the urea cycle. The first metabolic cycle to be discovered, it is used by land-dwelling vertebrates to convert ammonia, which is highly toxic, to urea for excretion. Now we’ll find 11 conserved quantities in the urea cycle, including 7 emergent ones.

...

Coupling Through Emergent Conservation Laws (Part 6)

joint post with Jonathan Lorand, Blake Pollard, and Maru Sarazola

Now let’s think about emergent conservation laws!

When a heavy rock connected to a lighter one by a pulley falls down and pulls up the lighter one, you’re seeing an emergent conservation law:

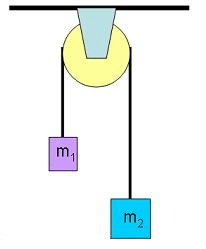
Here the height of the heavy rock plus the height of light one is a constant. That’s a conservation law! It forces some of the potential energy lost by one rock to be transferred to the other. But it’s not a fundamental conservation law,...