John C. Baez's Blog, page 54

Second Symposium on Compositional Structures

I’ve been asleep at the switch; this announcement is probably too late for anyone outside the UK. But still, it’s great to see how applied category theory is taking off! And this conference is part of a series, so if you miss this one you can still go to the next.

• Second Symposium on Compositional Structures (SYCO2), 17-18 December 2018, University of Strathclyde, Glasgow.

Accepted presentations

http://events.cs.bham.ac.uk/syco/2/accepted.html

Registration

Please register asap so that c...

Geometric Quantization (Part 1)

I can’t help thinking about geometric quantization. I feel it holds some lessons about the relation between classical and quantum mechanics that we haven’t fully absorbed yet. I want to play my cards fairly close to my chest, because there are some interesting ideas I haven’t fully explored yet… but still, there are also plenty of ‘well-known’ clues that I can afford to explain.

The first one is this. As beginners, we start by thinking of geometric quantization as a procedure for taking a sym...

Stratospheric Controlled Perturbation Experiment

I have predicted for a while that as the issue of climate change becomes ever more urgent, the public attitude regarding geoengineering will at some point undergo a phase transition. For a long time it seems the general attitude has been that deliberately interfering with the Earth’s climate on a large scale is “unthinkable”: beyond the pale. I predict that at some point this will flip and the general attitude will become: “how soon can we do it?”

The danger then is that we rush headlong into...

Category Theory Course

I’m teaching a course on category theory at U.C. Riverside, and since my website is still suffering from reduced functionality I’ll put the course notes here for now. I taught an introductory course on category theory in 2016, but this one is a bit more advanced.

The hand-written notes here are by Christian Williams. They are probably best seen as a reminder to myself as to what I’d like to include in a short book someday.

• Lecture 1 What is pure mathematics all about? The importance of free...

Lebesgue Universal Covering Problem (Part 3)

Back in 2015, I reported some progress on this difficult problem in plane geometry. I’m happy to report some more.

First, remember the story. A subset of the plane has diameter 1 if the distance between any two points in this set is ≤ 1. A a universal covering is a convex subset of the plane that can cover a translated, reflected and/or rotated version of every subset of the plane with diameter 1. In 1914, the famous mathematician Henri Lebesgue sent a letter to a fellow named Pál, challengin...

Riverside Math Workshop

We’re having a workshop with a bunch of cool math talks at U. C. Riverside, and you can register for it here:

• Riverside Mathematics Workshop for Excellence and Diversity, Friday 19 October – Saturday 20 October, 2018. Organized by John Baez, Carl Mautner, José González and Chen Weitao.

This is the first of an annual series workshop to showcase and celebrate excellence in research by women and other under-represented groups for the purpose of fostering and encouraging growth in the U.C. Rive...

Applied Category Theory 2019

[image error]

I’m helping organize ACT 2019, an applied category theory conference and school at Oxford, July 15-26, 2019.

More details will come later, but here’s the basic idea. If you’re a grad student interested in this subject, you should apply for the ‘school’. Not yet—we’ll let you know when.

Dear all,

As part of a new growing community in Applied Category Theory, now with a dedicated journal Compositionality, a traveling workshop series SYCO, a forthcoming Cambridge U. Press book series Reasonin...

Patterns That Eventually Fail

Sometimes patterns can lead you astray. For example, it’s known that

is a good approximation to the number of primes less than or equal to Numerical evidence suggests that 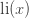is always greater than 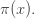For example,

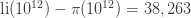
and

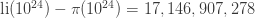
But in 1914, Littlewood heroically showed that in fact, changes sign infinitely many times!

This raised the question: when does 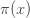first exceed 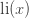? In 1933, Littlewood’s student Skewes showed, assuming the Riemann hypothesis, that it must do so for some less than or equal t...

What is Applied Category Theory?

Tai-Danae Bradley has a new free “booklet” on applied category theory. It was inspired by the workshop Applied Category Theory 2018, which she attended, and I think it makes a great complement to Fong and Spivak’s book Seven Sketches and my online course based on that book:

• Tai-Danae Bradley, What is Applied Category Theory?

Abstract. This is a collection of introductory, expository notes on applied category theory, inspired by the 2018 Applied Category Theory Workshop, and in these notes...

The 5/8 Theorem

This is a well-known, easy group theory result that I just learned. I would like to explain it more slowly and gently, and I hope memorably, than I’ve seen it done.

It’s called the 5/8 theorem. Randomly choose two elements of a finite group. What’s the probability that they commute? If it exceeds 62.5%, the group must be abelian!

This was probably known for a long time, but the first known proof appears in a paper by Erdös and Turan.

It’s fun to lead up to this proof by looking for groups tha...