Nicole Yunger Halpern's Blog, page 2

Quantum automata

Do you know when an engineer built the first artificial automaton—the first human-made machine that operated by itself, without external control mechanisms that altered the machine’s behavior over time as the machine undertook its mission?

The ancient Greek thinker Archytas of Tarentum reportedly created it about 2,300 years ago. Steam propelled his mechanical pigeon through the air.

For centuries, automata cropped up here and there as curiosities and entertainment. The wealthy exhibited automata to amuse and awe their peers and underlings. For instance, the French engineer Jacques de Vauconson built a mechanical duck that appeared to eat and then expel grains. The device earned the nickname the Digesting Duck…and the nickname the Defecating Duck.

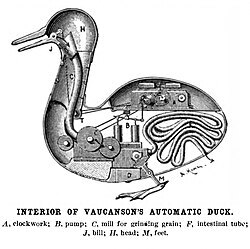
Vauconson also invented a mechanical loom that helped foster the Industrial Revolution. During the 18th and 19th centuries, automata began to enable factories, which changed the face of civilization. We’ve inherited the upshots of that change. Nowadays, cars drive themselves, Roombas clean floors, and drones deliver packages.1 Automata have graduated from toys to practical tools.2

Rather, classical automata have. What of their quantum counterparts?

Scientists have designed autonomous quantum machines, and experimentalists have begun realizing them. The roster of such machines includes autonomous quantum engines, refrigerators, and clocks. Much of this research falls under the purview of quantum thermodynamics, due to the roles played by energy in these machines’ functioning: above, I defined an automaton as a machine free of time-dependent control (exerted by a user). Equivalently, according to a thermodynamicist mentality, we can define an automaton as a machine on which no user performs any work as the machine operates. Thermodynamic work is well-ordered energy that can be harnessed directly to perform a useful task. Often, instead of receiving work, an automaton receives access to a hot environment and a cold environment. Heat flows from the hot to the cold, and the automaton transforms some of the heat into work.

Quantum automata appeal to me because quantum thermodynamics has few practical applications, as I complained in my previous blog post. Quantum thermodynamics has helped illuminate the nature of the universe, and I laud such foundational insights. Yet we can progress beyond laudation by trying to harness those insights in applications. Some quantum thermal machines—quantum batteries, engines, etc.—can outperform their classical counterparts, according to certain metrics. But controlling those machines, and keeping them cold enough that they behave quantum mechanically, costs substantial resources. The machines cost more than they’re worth. Quantum automata, requiring little control, offer hope for practicality. 

To illustrate this hope, my group partnered with Simone Gasparinetti’s lab at Chalmer’s University in Sweden. The experimentalists created an autonomous quantum refrigerator from superconducting qubits. The quantum refrigerator can help reset, or “clear,” a quantum computer between calculations.

Artist’s conception of the autonomous-quantum-refrigerator chip. Credit: Chalmers University of Technology/Boid AB/NIST.

After we wrote the refrigerator paper, collaborators and I raised our heads and peered a little farther into the distance. What does building a useful autonomous quantum machine take, generally? Collaborators and I laid out guidelines in a “Key Issues Review” published in Reports in Progress on Physics last November.

We based our guidelines on DiVincenzo’s criteria for quantum computing. In 1996, David DiVincenzo published seven criteria that any platform, or setup, must meet to serve as a quantum computer. He cast five of the criteria as necessary and two criteria, related to information transmission, as optional. Similarly, our team provides ten criteria for building useful quantum automata. We regard eight of the criteria as necessary, at least typically. The final two, optional guidelines govern information transmission and machine transportation. 

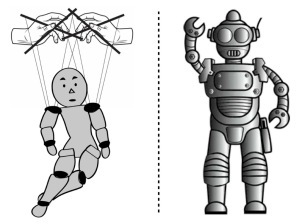Time-dependent external control and autonomy

DiVincenzo illustrated his criteria with multiple possible quantum-computing platforms, such as ions. Similarly, we illustrate our criteria in two ways. First, we show how different quantum automata—engines, clocks, quantum circuits, etc.—can satisfy the criteria. Second, we illustrate how quantum automata can consist of different platforms: ultracold atoms, superconducting qubits, molecules, and so on.

Nature has suggested some of these platforms. For example, our eyes contain autonomous quantum energy transducers called photoisomers, or molecular switches. Suppose that such a molecule absorbs a photon. The molecule may use the photon’s energy to switch configuration. This switching sets off chemical and neurological reactions that result in the impression of sight. So the quantum switch transduces energy from light into mechanical, chemical, and electric energy.

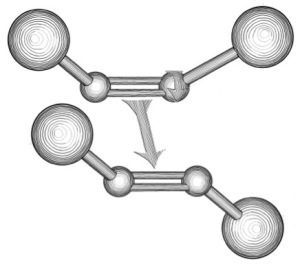Photoisomer. (Image by Todd Cahill, from Quantum Steampunk.)

My favorite of our criteria ranks among the necessary conditions: every useful quantum automata must produce output worth the input. How one quantifies a machine’s worth and cost depends on the machine and on the user. For example, an agent using a quantum engine may care about the engine’s efficiency, power, or efficiency at maximum power. Costs can include the energy required to cool the engine to the quantum regime, as well as the control required to initialize the engine. The agent also chooses which value they regard as an acceptable threshold for the output produced per unit input. I like this criterion because it applies a broom to dust that we quantum thermodynamicists often hide under a rug: quantum thermal machines’ costs. Let’s begin building quantum engines that perform more work than they require to operate.

One might object that scientists and engineers are already sweating over nonautonomous quantum machines. Companies, governments, and universities are pouring billions of dollars into quantum computing. Building a full-scale quantum computer by hook or by crook, regardless of classical control, is costing enough. Eliminating time-dependent control sounds even tougher. Why bother?

Fellow Quantum Frontiers blogger John Preskill pointed out one answer, when I described my new research program to him in 2022: control systems are classical—large and hot. Consider superconducting qubits—tiny quantum circuits—printed on a squarish chip about the size of your hand. A control wire terminates on each qubit. The rest of the wire runs off the edge of the chip, extending to classical hardware standing nearby. One can fit only so many wires on the chip, so one can fit only so many qubits. Also, the wires, being classical, are hotter than the qubits should be. The wires can help decohere the circuits, introducing errors into the quantum information they store. The more we can free the qubits from external control—the more autonomy we can grant them—the better.

Besides, quantum automata exemplify quantum steampunk, as my coauthor Pauli Erker observed. I kicked myself after he did, because I’d missed the connection. The irony was so thick, you could have cut it with the retractible steel knife attached to a swashbuckling villain’s robotic arm. Only two years before, I’d read The Watchmaker of Filigree Street, by Natasha Pulley. The novel features a Londoner expatriate from Meiji Japan, named Mori, who builds clockwork devices. The most endearing is a pet-like octopus, called Katsu, who scrambles around Mori’s workshop and hoards socks. 

Does the world need a quantum version of Katsu? Not outside of quantum-steampunk fiction…yet. But a girl can dream. And quantum automata now have the opportunity to put quantum thermodynamics to work.

From tumblr

1And deliver pizzas. While visiting the University of Pittsburgh a few years ago, I was surprised to learn that the robots scurrying down the streets were serving hungry students.

2And minions of starving young scholars.

Quantum Algorithms: A Call To Action

Quantum computing finds itself in a peculiar situation. On the technological side, after billions of dollars and decades of research, working quantum computers are nearing fruition. But still, the number one question asked about quantum computers is the same as it was two decades ago: What are they good for? The honest answer reveals an elephant in the room: We don’t fully know yet. For theorists like me, this is an opportunity, a call to action.

Technological momentum

Suppose we do not have quantum computers in a few decades time. What will be the reason? It’s unlikely that we’ll encounter some insurmountable engineering obstacle. The theoretical basis of quantum error-correction is solid, and several platforms are now below the error-correction threshold (Harvard, Yale, Google). Experimentalists believe today’s technology can scale to 100 logical qubits and 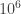gates—the megaquop era. If mankind spends $100 billion over the next few decades, it’s likely we could build a quantum computer.

A more concerning reason that quantum computing might fail is that there is not enough incentive to justify such a large investment in R&D and infrastructure. Let’s make a comparison to nuclear fusion. Like quantum hardware, they have challenging science and engineering problems to solve. However, if a nuclear fusion lab were to succeed in their mission of building a nuclear fusion reactor, the application would be self-evident. This is not the case for quantum computing—it is a sledgehammer looking for nails to hit.

Nevertheless, industry investment in quantum computing is currently accelerating. To maintain the momentum, it is critical to match investment growth and hardware progress with algorithmic capabilities. The time to discover quantum algorithms is now.

Empowered theorists

Theory research is forward-looking and predictive. Theorists such as Geoffrey Hinton laid the foundations of the current AI revolution. But decades later, with an abundance of computing hardware, AI has become much more of an empirical field. I look forward to the day that quantum hardware reaches a state of abundance, but that day is not yet here.

Today, quantum computing is an area where theorists have extraordinary leverage. A few pages of mathematics by Peter Shor inspired thousands of researchers, engineers and investors to join the field. Perhaps another few pages by someone reading this blog will establish a future of world-altering impact for the industry. There are not many places where mathematics has such potential for influence. An entire community of experimentalists, engineers, and businesses are looking to the theorists for ideas.

The Challenge

Traditionally, it is thought that the ideal quantum algorithm would exhibit three features. First, it should be provably correct, giving a guarantee that executing the quantum circuit reliably will achieve the intended outcome. Second, the underlying problem should be classically hard—the output of the quantum algorithm should be computationally hard to replicate with a classical algorithm. Third, it should be useful, with the potential to solve a problem of interest in the real world. Shor’s algorithm comes close to meeting all of these criteria. However, demanding all three in an absolute fashion may be unnecessary and perhaps even counterproductive to progress.

Provable correctness is important, since today we cannot yet empirically test quantum algorithms on hardware at scale. But what degree of evidence should we require for classical hardness? Rigorous proof of classical hardness is currently unattainable without resolving major open problems like P vs NP, but there are softer forms of proof, such as reductions to well-studied classical hardness assumptions.

I argue that we should replace the ideal of provable hardness with a more pragmatic approach: The quantum algorithm should outperform the best known classical algorithm that produces the same output by a super-quadratic speedup.1 Emphasizing provable classical hardness might inadvertently impede the discovery of new quantum algorithms, since a truly novel quantum algorithm could potentially introduce a new classical hardness assumption that differs fundamentally from established ones. The back-and-forth process of proposing and breaking new assumptions is a productive direction that helps us triangulate where quantum advantage lies.

It may also be an unproductive strategy to aim directly at solving existing real-world problems with quantum algorithms. Fundamental computational tasks with quantum advantage are special and we have very few examples, yet they necessarily provide the basis for any eventual quantum application. We should search for more of these fundamental tasks and match them to applications later.

That said, it is important to distinguish between quantum algorithms that could one day provide the basis for a practically relevant computation, and those that will not. In the real world, computations are not useful unless they are verifiable or at least repeatable. For instance, consider a quantum simulation algorithm that computes a physical observable. If two different quantum computers run the simulation and get the same answer, one can be confident that this answer is correct and that it makes a robust prediction about the world. Some problems such as factoring are naturally easy to verify classically, but we can set the bar even lower: The output of a useful quantum algorithm should at least be repeatable by another quantum computer.

There is a subtle fourth requirement of paramount importance that is often overlooked, captured by the following litmus test: If given a quantum computer tomorrow, could you implement your quantum algorithm? In order to do so, you need not only a quantum algorithm but also a distribution over its inputs on which to run it. Classical hardness must then be judged in the average case over this distribution of inputs, rather than in the worst case.

I’ll end this section with a specific caution regarding quantum algorithms whose output is the expectation value of an observable. A common reason these proposals fail to be classically hard is that the expectation value exponentially concentrates over the distribution of inputs. When this happens, a trivial classical algorithm can replicate the quantum result by simply outputting the concentrated (typical) value for every input. To avoid this, we must seek ensembles of quantum circuits whose expectation values exhibit meaningful variation and sensitivity to different inputs.

We can crystallize these priorities into the following challenge:

The Challenge
Find a quantum algorithm and a distribution over its inputs with the following features:
— (Provable correctness.) The quantum algorithm is provably correct.
— (Classical hardness.) The quantum algorithm outperforms the best known classical algorithm that performs the same task by a super-quadratic speedup, in the average-case over the distribution of inputs.
— (Potential utility.) The output is verifiable, or at least repeatable.

Examples and non-examplesCategoryClassically verifiableQuantumly repeatablePotentially usefulProvable classical hardnessExamplesSearch problemYesYesYesNoShor ‘99

Regev’s reduction: CLZ22, YZ24, Jor+24

Planted inference: Has20, SOKB24Compute a valueNoYesYesNoCondensed matter physics?

Quantum chemistry?Proof of quantumnessYes, with keyYes, with respect to keyNoYes, under crypto assumptionsBCMVV21SamplingNoNoNoAlmost, under complexity assumptionsBJS10, AA11, Google ‘20We can categorize quantum algorithms by the form of their output. First, there are quantum algorithms for search problems, which produce a bitstring satisfying some constraints. This could be the prime factors of a number, a planted feature in some dataset, or the solution to an optimization problem. Next, there are quantum algorithms that compute a value to some precision, for example the expectation value of some physical observable. Then there are proofs of quantumness, which involve a verifier who generates a test using some hidden key, and the key can be used to verify the output. Finally, there are quantum algorithms which sample from some distribution.

Hamiltonian simulation is perhaps the most widely heralded source of quantum utility. Physics and chemistry contain many quantities that Nature computes effortlessly, yet remain beyond the reach of even our best classical simulations. Quantum computation is capable of simulating Nature directly, giving us strong reason to believe that quantum algorithms can compute classically-hard quantities.

There are already many examples where a quantum computer could help us answer an unsolved scientific question, like determining the phase diagram of the Hubbard model or the ground energy of FeMoCo. These undoubtedly have scientific value. However, they are isolated examples, whereas we would like evidence that the pool of quantum-solvable questions is inexhaustible. Can we take inspiration from strongly correlated physics to write down a concrete ensemble of Hamiltonian simulation instances where there is a classically-hard observable? This would gather evidence for the sustained, broad utility of quantum simulation, and would also help us understand where and how quantum advantage arises.

Over in the computer science community, there has been a lot of work on oracle separations such as welded trees and forrelation, which should give us confidence in the abilities of quantum computers. Can we instantiate these oracles in a way that pragmatically remains classically hard? This is necessary in order to pass our earlier litmus test of being ready to run the quantum algorithm tomorrow.

In addition to Hamiltonian simulation, there are several other broad classes of quantum algorithms, including quantum algorithms for linear systems of equations and differential equations, variational quantum algorithms for machine learning, and quantum algorithms for optimization. These frameworks sometimes come with proofs of BQP-completeness.

The issue with these broad frameworks is that they often do not specify a distribution over inputs. Can we find novel ensembles of inputs to these frameworks which exhibit super-quadratic speedups? BQP-completeness shows that one has translated the notion of quantum computation into a different language, which allows one to embed an existing quantum algorithm such as Shor’s algorithm into your framework. But in order to discover a new quantum algorithm, you must find an ensemble of BQP computations which does not arise from Shor’s algorithm.

Table I claims that sampling tasks alone are not useful since they are not even quantumly repeatable. One may wonder if sampling tasks could be useful in some way. After all, classical Monte Carlo sampling algorithms are widely used in practice. However, applications of sampling typically use samples to extract meaningful information or specific features of the underlying distribution. For example, Monte Carlo sampling can be used to evaluate integrals in Bayesian inference and statistical physics. In contrast, samples obtained from random quantum circuits lack any discernible features. If a collection of quantum algorithms generated samples containing meaningful signals from which one could extract classically hard-to-compute values, those algorithms would effectively transition into the compute a value category.

Table I also claims that proofs of quantumness are not useful. This is not completely true—one potential application is generating certifiable randomness. However, such applications are generally cryptographic rather than computational in nature. Specifically, proofs of quantumness cannot help us solve problems or answer questions whose solutions we do not already know.

Finally, there are several exciting directions proposing applications of quantum technologies in sensing and metrology, communication, learning with quantum memory, and streaming. These are very interesting, and I hope that mankind’s second century of quantum mechanics brings forth all flavors of capabilities. However, the technological momentum is mostly focused on building quantum computers for the purpose of computational advantage, and so this is where breakthroughs will have the greatest immediate impact.

Don’t be too afraid

At the annual QIP conference, only a handful of papers out of hundreds each year attempt to advance new quantum algorithms. Given the stakes, why is this number so low? One common explanation is that quantum algorithm research is simply too difficult. Nevertheless, we have seen substantial progress in quantum algorithms in recent years. After an underwhelming lack of end-to-end proposals with the potential for utility between the years 2000 and 2020, Table I exhibits several breakthroughs from the past 5 years.

In between blind optimism and resigned pessimism, embracing a mission-driven mindset can propel our field forward. We should allow ourselves to adopt a more exploratory, scrappier approach: We can hunt for quantum advantages in yet-unstudied problems or subtle signals in the third decimal place. The bar for meaningful progress is lower than it might seem, and even incremental advances are valuable. Don’t be too afraid!

Quadratic speedups are widespread but will not form the basis of practical quantum advantage due to the overheads associated with quantum error-correction. ︎

How writing a popular-science book led to a Nature Physics paper

Several people have asked me whether writing a popular-science book has fed back into my research. Nature Physics published my favorite illustration of the answer this January. Here’s the story behind the paper.

In late 2020, I was sitting by a window in my home office (AKA living room) in Cambridge, Massachusetts. I’d drafted 15 chapters of my book Quantum Steampunk. The epilogue, I’d decided, would outline opportunities for the future of quantum thermodynamics. So I had to come up with opportunities for the future of quantum thermodynamics. The rest of the book had related foundational insights provided by quantum thermodynamics about the universe’s nature. For instance, quantum thermodynamics had sharpened the second law of thermodynamics, which helps explain time’s arrow, into more-precise statements. Conventional thermodynamics had not only provided foundational insights, but also accompanied the Industrial Revolution, a paragon of practicality. Could quantum thermodynamics, too, offer practical upshots?

Quantum thermodynamicists had designed quantum engines, refrigerators, batteries, and ratchets. Some of these devices could outperform their classical counterparts, according to certain metrics. Experimentalists had even realized some of these devices. But the devices weren’t useful. For instance, a simple quantum engine consisted of one atom. I expected such an atom to produce one electronvolt of energy per engine cycle. (A light bulb emits about 1021 electronvolts of light per second.) Cooling the atom down and manipulating it would cost loads more energy. The engine wouldn’t earn its keep.

Autonomous quantum machines offered greater hope for practicality. By autonomous, I mean, not requiring time-dependent external control: nobody need twiddle knobs or push buttons to guide the machine through its operation. Such control requires work—organized, coordinated energy. Rather than receiving work, an autonomous machine accesses a cold environment and a hot environment. Heat—random, disorganized energy cheaper than work—flows from the hot to the cold. The machine transforms some of that heat into work to power itself. That is, the machine sources its own work from cheap heat in its surroundings. Some air conditioners operate according to this principle. So can some quantum machines—autonomous quantum machines.

Thermodynamicists had designed autonomous quantum engines and refrigerators. Trapped-ion experimentalists had realized one of the refrigerators, in a groundbreaking result. Still, the autonomous quantum refrigerator wasn’t practical. Keeping the ion cold and maintaining its quantum behavior required substantial work.

My community needed, I wrote in my epilogue, an analogue of solar panels in southern California. (I probably drafted the epilogue during a Boston winter, thinking wistfully of Pasadena.) If you built a solar panel in SoCal, you could sit back and reap the benefits all year. The panel would fulfill its mission without further effort from you. If you built a solar panel in Rochester, you’d have to scrape snow off of it. Also, the panel would provide energy only a few months per year. The cost might not outweigh the benefit. Quantum thermal machines resembled solar panels in Rochester, I wrote. We needed an analogue of SoCal: an appropriate environment. Most of it would be cold (unlike SoCal), so that maintaining a machine’s quantum nature would cost a user almost no extra energy. The setting should also contain a slightly warmer environment, so that net heat would flow. If you deposited an autonomous quantum machine in such a quantum SoCal, the machine would operate on its own.

Where could we find a quantum SoCal? I had no idea.

Sunny SoCal. (Specifically, the Huntington Gardens.)

A few months later, I received an email from quantum experimentalist Simone Gasparinetti. He was setting up a lab at Chalmers University in Sweden. What, he asked, did I see as opportunities for experimental quantum thermodynamics? We’d never met, but we agreed to Zoom. Quantum Steampunk on my mind, I described my desire for practicality. I described autonomous quantum machines. I described my yearning for a quantum SoCal.

I have it, Simone said.

Simone and his colleagues were building a quantum computer using superconducting qubits. The qubits fit on a chip about the size of my hand. To keep  the chip cold, the experimentalists put it in a dilution refrigerator. You’ve probably seen photos of dilution refrigerators from Google, IBM, and the like. The fridges tend to be cylindrical, gold-colored monstrosities from which wires stick out. (That is, they look steampunk.) You can easily develop the impression that the cylinder is a quantum computer, but it’s only the fridge.

Not a quantum computer

The fridge, Simone said, resembles an onion: it has multiple layers. Outer layers are warmer, and inner layers are colder. The quantum computer sits in the innermost layer, so that it behaves as quantum mechanically as possible. But sometimes, even the fridge doesn’t keep the computer cold enough.

Imagine that you’ve finished one quantum computation and you’re preparing for the next. The computer has written quantum information to certain qubits, as you’ve probably written on scrap paper while calculating something in a math class. To prepare for your next math assignment, given limited scrap paper, you’d erase your scrap paper. The quantum computer’s qubits need erasing similarly. Erasing, in this context, means cooling down even more than the dilution refrigerator can manage. 

Why not use an autonomous quantum refrigerator to cool the scrap-paper qubits?

I loved the idea, for three reasons. First, we could place the quantum refrigerator beside the quantum computer. The dilution refrigerator would already be cold, for the quantum computations’ sake. Therefore, we wouldn’t have to spend (almost any) extra work on keeping the quantum refrigerator cold. Second, Simone could connect the quantum refrigerator to an outer onion layer via a cable. Heat would flow from the warmer outer layer to the colder inner layer. From the heat, the quantum refrigerator could extract work. The quantum refrigerator would use that work to cool computational qubits—to erase quantum scrap paper. The quantum refrigerator would service the quantum computer. So, third, the quantum refrigerator would qualify as practical.

Over the next three years, we brought that vision to life. (By we, I mostly mean Simone’s group, as my group doesn’t have a lab.)

Artist’s conception of the autonomous-quantum-refrigerator chip. Credit: Chalmers University of Technology/Boid AB/NIST.

Postdoc Aamir Ali spearheaded the experiment. Then-master’s student Paul Jamet Suria and PhD student Claudia Castillo-Moreno assisted him. Maryland postdoc Jeffrey M. Epstein began simulating the superconducting qubits numerically, then passed the baton to PhD student José Antonio Marín Guzmán. 

The experiment provided a proof of principle: it demonstrated that the quantum refrigerator could operate. The experimentalists didn’t apply the quantum refrigerator in a quantum computation. Also, they didn’t connect the quantum refrigerator to an outer onion layer. Instead, they pumped warm photons to the quantum refrigerator via a cable. But even in such a stripped-down experiment, the quantum refrigerator outperformed my expectations. I thought it would barely lower the “scrap-paper” qubit’s temperature. But that qubit reached a temperature of 22 milliKelvin (mK). For comparison: if the qubit had merely sat in the dilution refrigerator, it would have reached a temperature of 45–70 mK. State-of-the-art protocols had lowered scrap-paper qubits’ temperatures to 40–49 mK. So our quantum refrigerator outperformed our competitors, through the lens of temperature. (Our quantum refrigerator cooled more slowly than they did, though.)

Simone, José Antonio, and I have followed up on our autonomous quantum refrigerator with a forward-looking review about useful autonomous quantum machines. Keep an eye out for a blog post about the review…and for what we hope grows into a subfield.

In summary, yes, publishing a popular-science book can benefit one’s research.

The first and second centuries of quantum mechanics

At this week’s American Physical Society Global Physics Summit in Anaheim, California, John Preskill spoke at an event celebrating 100 years of groundbreaking advances in quantum mechanics. Here are his remarks.

Welcome, everyone, to this celebration of 100 years of quantum mechanics hosted by the Physical Review Journals. I’m John Preskill and I’m honored by this opportunity to speak today. I was asked by our hosts to express some thoughts appropriate to this occasion and to feel free to share my own personal journey as a physicist. I’ll embrace that charge, including the second part of it, perhaps even more that they intended. But over the next 20 minutes I hope to distill from my own experience some lessons of broader interest.

I began graduate study in 1975, the midpoint of the first 100 years of quantum mechanics, 50 years ago and 50 years after the discovery of quantum mechanics in 1925 that we celebrate here. So I’ll seize this chance to look back at where quantum physics stood 50 years ago, how far we’ve come since then, and what we can anticipate in the years ahead.

As an undergraduate at Princeton, I had many memorable teachers; I’ll mention just one: John Wheeler, who taught a full-year course for sophomores that purported to cover all of physics. Wheeler, having worked with Niels Bohr on nuclear fission, seemed implausibly old, though he was actually 61. It was an idiosyncratic course, particularly because Wheeler did not refrain from sharing with the class his current research obsessions. Black holes were a topic he shared with particular relish, including the controversy at the time concerning whether evidence for black holes had been seen by astronomers. Especially notably, when covering the second law of thermodynamics, he challenged us to ponder what would happen to entropy lost behind a black hole horizon, something that had been addressed by Wheeler’s graduate student Jacob Bekenstein, who had finished his PhD that very year. Bekenstein’s remarkable conclusion that black holes have an intrinsic entropy proportional to the event horizon area delighted the class, and I’ve had had many occasions to revisit that insight in the years since then. The lesson being that we should not underestimate the potential impact of sharing our research ideas with undergraduate students.

Stephen Hawking made that connection between entropy and area precise the very next year when he discovered that black holes radiate; his resulting formula for black hole entropy, a beautiful synthesis of relativity, quantum theory, and thermodynamics ranks as one of the shining achievements in the first 100 years of quantum mechanics. And it raised a deep puzzle pointed out by Hawking himself with which we have wrestled since then, still without complete success — what happens to information that disappears inside black holes?

Hawking’s puzzle ignited a titanic struggle between cherished principles. Quantum mechanics tells us that as quantum systems evolve, information encoded in a system can get scrambled into an unrecognizable form, but cannot be irreversibly destroyed. Relativistic causality tells us that information that falls into a black hole, which then evaporates, cannot possibly escape and therefore must be destroyed. Who wins – quantum theory or causality? A widely held view is that quantum mechanics is the victor, that causality should be discarded as a fundamental principle. This calls into question the whole notion of spacetime — is it fundamental, or an approximate property that emerges from a deeper description of how nature works? If emergent, how does it emerge and from what? Fully addressing that challenge we leave to the physicists of the next quantum century.

I made it to graduate school at Harvard and the second half century of quantum mechanics ensued. My generation came along just a little too late to take part in erecting the standard model of particle physics, but I was drawn to particle physics by that intoxicating experimental and theoretical success. And many new ideas were swirling around in the mid and late 70s of which I’ll mention only two. For one, appreciation was growing for the remarkable power of topology in quantum field theory and condensed matter, for example the theory of topological solitons. While theoretical physics and mathematics had diverged during the first 50 years of quantum mechanics, they have frequently crossed paths in the last 50 years, and topology continues to bring both insight and joy to physicists. The other compelling idea was to seek insight into fundamental physics at very short distances by searching for relics from the very early history of the universe. My first publication resulted from contemplating a question that connected topology and cosmology: Would magnetic monopoles be copiously produced in the early universe? To check whether my ideas held water, I consulted not a particle physicist or a cosmologist, but rather a condensed matter physicist (Bert Halperin) who provided helpful advice. The lesson being that scientific opportunities often emerge where different subfields intersect, a realization that has helped to guide my own research over the following decades.

Looking back at my 50 years as a working physicist, what discoveries can the quantumists point to with particular pride and delight?

I was an undergraduate when Phil Anderson proclaimed that More is Different, but as an arrogant would be particle theorist at the time I did not appreciate how different more can be. In the past 50 years of quantum mechanics no example of emergence was more stunning than the fractional quantum Hall effect. We all know full well that electrons are indivisible particles. So how can it be that in a strongly interacting two-dimensional gas an electron can split into quasiparticles each carrying a fraction of its charge? The lesson being: in a strongly-correlated quantum world, miracles can happen. What other extraordinary quantum phases of matter await discovery in the next quantum century?

Another thing I did not adequately appreciate in my student days was atomic physics. Imagine how shocked those who elucidated atomic structure in the 1920s would be by the atomic physics of today. To them, a quantum measurement was an action performed on a large ensemble of similarly prepared systems. Now we routinely grab ahold of a single atom, move it, excite it, read it out, and induce pairs of atoms to interact in precisely controlled ways. When interest in quantum computing took off in the mid-90s, it was ion-trap clock technology that enabled the first quantum processors. Strong coupling between single photons and single atoms in optical and microwave cavities led to circuit quantum electrodynamics, the basis for today’s superconducting quantum computers. The lesson being that advancing our tools often leads to new capabilities we hadn’t anticipated. Now clocks are so accurate that we can detect the gravitational redshift when an atom moves up or down by a millimeter in the earth’s gravitational field. Where will the clocks of the second quantum century take us?

Surely one of the great scientific triumphs of recent decades has been the success of LIGO, the laser interferometer gravitational-wave observatory. If you are a gravitational wave scientist now, your phone buzzes so often to announce another black hole merger that it’s become annoying. LIGO would not be possible without advanced laser technology, but aside from that what’s quantum about LIGO? When I came to Caltech in the early 1980s, I learned about a remarkable idea (from Carl Caves) that the sensitivity of an interferometer can be enhanced by a quantum strategy that did not seem at all obvious — injecting squeezed vacuum into the interferometer’s dark port. Now, over 40 years later, LIGO improves its detection rate by using that strategy. The lesson being that theoretical insights can enhance and transform our scientific and technological tools. But sometimes that takes a while.

What else has changed since 50 years ago? Let’s give thanks for the arXiv. When I was a student few scientists would type their own technical papers. It took skill, training, and patience to operate the IBM typewriters of the era. And to communicate our results, we had no email or world wide web. Preprints arrived by snail mail in Manila envelopes, if you were lucky enough to be on the mailing list. The Internet and the arXiv made scientific communication far faster, more convenient, and more democratic, and LaTeX made producing our papers far easier as well. And the success of the arXiv raises vexing questions about the role of journal publication as the next quantum century unfolds.

I made a mid-career shift in research direction, and I’m often asked how that came about. Part of the answer is that, for my generation of particle physicists, the great challenge and opportunity was to clarify the physics beyond the standard model, which we expected to provide a deeper understanding of how nature works. We had great hopes for the new phenomenology that would be unveiled by the Superconducting Super Collider, which was under construction in Texas during the early 90s. The cancellation of that project in 1993 was a great disappointment. The lesson being that sometimes our scientific ambitions are thwarted because the required resources are beyond what society will support. In which case, we need to seek other ways to move forward.

And then the next year, Peter Shor discovered the algorithm for efficiently finding the factors of a large composite integer using a quantum computer. Though computational complexity had not been part of my scientific education, I was awestruck by this discovery. It meant that the difference between hard and easy problems — those we can never hope to solve, and those we can solve with advanced technologies — hinges on our world being quantum mechanical. That excited me because one could anticipate that observing nature through a computational lens would deepen our understanding of fundamental science. I needed to work hard to come up to speed in a field that was new to me — teaching a course helped me a lot.

Ironically, for 4 ½ years in the mid-1980s I sat on the same corridor as Richard Feynman, who had proposed the idea of simulating nature with quantum computers in 1981. And I never talked to Feynman about quantum computing because I had little interest in that topic at the time. But Feynman and I did talk about computation, and in particular we were both very interested in what one could learn about quantum chromodynamics from Euclidean Monte Carlo simulations on conventional computers, which were starting to ramp up in that era. Feynman correctly predicted that it would be a few decades before sufficient computational power would be available to make accurate quantitative predictions about nonperturbative QCD. But it did eventually happen — now lattice QCD is making crucial contributions to the particle physics and nuclear physics programs. The lesson being that as we contemplate quantum computers advancing our understanding of fundamental science, we should keep in mind a time scale of decades.

Where might the next quantum century take us? What will the quantum computers of the future look like, or the classical computers for that matter? Surely the qubits of 100 years from now will be much different and much better than what we have today, and the machine architecture will no doubt be radically different than what we can currently envision. And how will we be using those quantum computers? Will our quantum technology have transformed medicine and neuroscience and our understanding of living matter? Will we be building materials with astonishing properties by assembling matter atom by atom? Will our clocks be accurate enough to detect the stochastic gravitational wave background and so have reached the limit of accuracy beyond which no stable time standard can even be defined? Will quantum networks of telescopes be observing the universe with exquisite precision and what will that reveal? Will we be exploring the high energy frontier with advanced accelerators like muon colliders and what will they teach us? Will we have identified the dark matter and explained the dark energy? Will we have unambiguous evidence of the universe’s inflationary origin? Will we have computed the parameters of the standard model from first principles, or will we have convinced ourselves that’s a hopeless task? Will we have understood the fundamental constituents from which spacetime itself is composed?

There is an elephant in the room. Artificial intelligence is transforming how we do science at a blistering pace. What role will humans play in the advancement of science 100 years from now? Will artificial intelligence have melded with quantum intelligence? Will our instruments gather quantum data Nature provides, transduce it to quantum memories, and process it with quantum computers to discern features of the world that would otherwise have remained deeply hidden?

To a limited degree, in contemplating the future we are guided by the past. Were I asked to list the great ideas about physics to surface over the 50-year span of my career, there are three in particular I would nominate for inclusion on that list. (1) The holographic principle, our best clue about how gravity and quantum physics fit together. (2) Topological quantum order, providing ways to distinguish different phases of quantum matter when particles strongly interact with one another. (3) And quantum error correction, our basis for believing we can precisely control very complex quantum systems, including advanced quantum computers. It’s fascinating that these three ideas are actually quite closely related. The common thread connecting them is that all relate to the behavior of many-particle systems that are highly entangled.

Quantum error correction is the idea that we can protect quantum information from local noise by encoding the information in highly entangled states such that the protected information is inaccessible locally, when we look at just a few particles at a time. Topological quantum order is the idea that different quantum phases of matter can look the same when we observe them locally, but are distinguished by global properties hidden from local probes — in other words such states of matter are quantum memories protected by quantum error correction. The holographic principle is the idea that all the information in a gravitating three-dimensional region of space can be encoded by mapping it to a local quantum field theory on the two-dimensional boundary of the space. And that map is in fact the encoding map of a quantum error-correcting code. These ideas illustrate how as our knowledge advances, different fields of physics are converging on common principles. Will that convergence continue in the second century of quantum mechanics? We’ll see.

As we contemplate the long-term trajectory of quantum science and technology, we are hampered by our limited imaginations. But one way to loosely characterize the difference between the past and the future of quantum science is this: For the first hundred years of quantum mechanics, we achieved great success at understanding the behavior of weakly correlated many-particles systems relevant to for example electronic structure, atomic and molecular physics, and quantum optics. The insights gained regarding for instance how electrons are transported through semiconductors or how condensates of photons and atoms behave had invaluable scientific and technological impact. The grand challenge and opportunity we face in the second quantum century is acquiring comparable insight into the complex behavior of highly entangled states of many particles which are well beyond the reach of current theory or computation. This entanglement frontier is vast, inviting, and still largely unexplored. The wonders we encounter in the second century of quantum mechanics, and their implications for human civilization, are bound to supersede by far those of the first century. So let us gratefully acknowledge the quantum heroes of the past and present, and wish good fortune to the quantum explorers of the future.

Image credit: Jorge Cham

Developing an AI for Quantum Chess: Part 1

In January 2016, Caltech’s Institute for Quantum Information and Matter unveiled a YouTube video featuring an extraordinary chess showdown between actor Paul Rudd (a.k.a. Ant-Man) and the legendary Dr. Stephen Hawking. But this was no ordinary match—Rudd had challenged Hawking to a game of Quantum Chess. At the time, Fast Company remarked, “Here we are, less than 10 days away from the biggest advertising football day of the year, and one of the best ads of the week is a 12-minute video of quantum chess from Caltech.” But a Super Bowl ad for what, exactly?

For the past nine years, Quantum Realm Games, with continued generous support from IQIM and other strategic partnerships, has been tirelessly refining the rudimentary Quantum Chess prototype showcased in that now-viral video, transforming it into a fully realized game—one you can play at home or even on a quantum computer. And now, at long last, we’ve reached a major milestone: the launch of Quantum Chess 1.0. You might be wondering—what took us so long?

The answer is simple: developing an AI capable of playing Quantum Chess.

Before we dive into the origin story of the first-ever AI designed to master a truly quantum game, it’s important to understand what enables modern chess AI in the first place.

Chess AI is a vast and complex field, far too deep to explore in full here. For those eager to delve into the details, the Chess Programming Wiki serves as an excellent resource. Instead, this post will focus on what sets Quantum Chess AI apart from its classical counterpart—and the unique challenges we encountered along the way.

So, let’s get started!

Depth Matters credit: https://www.freecodecamp.org/news/simple-chess-ai-step-by-step-1d55a9266977/

With Chess AI, the name of the game is “depth”, at least for versions based on the Minimax strategy conceived by John von Neumann in 1928 (we’ll say a bit about Neural Network based AI later). The basic idea is that the AI will simulate the possible moves each player can make, down to some depth (number of moves) into the future, then decide which one is best based on a set of evaluation criteria (minimizing the maximum loss incurred by the opponent). The faster it can search, the deeper it can go. And the deeper it can go, the better its evaluation of each potential next move is.

Searching into the future can be modelled as a branching tree, where each branch represents a possible move from a given position (board configuration). The average branching factor for chess is about 35. That means that for a given board configuration, there are about 35 different moves to choose from. So if the AI looks 2 ply (moves) ahead, it sees 35×35 moves on average, and this blows up quickly. By 4 ply, the AI already has 1.5 million moves to evaluate. 

Modern chess engines, like Stockfish and Leela, gain their strength by looking far into the future. Depth 10 is considered low in these cases; you really need 20+ if you want the engine to return an accurate evaluation of each move under consideration. To handle that many evaluations, these engines use strong heuristics to prune branches (the width of the tree), so that they don’t need to calculate the exponentially many leaves of the tree. For example, if one of the branches involves losing your Queen, the algorithm may decide to prune that branch and all the moves that come after. But as experienced players can see already, since a Queen sacrifice can sometimes lead to massive gains down the road, such a “naive” heuristic may need to be refined further before it is implemented. Even so, the tension between depth-first versus breadth-first search is ever present.

So I heard you like branches… https://www.sciencenews.org/article/leonardo-da-vinci-rule-tree-branch-wrong-limb-area-thickness

The addition of split and merge moves in Quantum Chess absolutely explodes the branching factor. Early simulations have shown that it may be in the range of 100-120, but more work is needed to get an accurate count. For all we know, branching could be much bigger. We can get a sense by looking at a single piece, the Queen.

On an otherwise empty chess board, a single Queen on d4 has 27 possible moves (we leave it to the reader to find them all). In Quantum Chess, we add the split move: every piece, besides pawns, can move to any two empty squares it can reach legally. This adds every possible paired combination of standard moves to the list. 

But wait, there’s more! 

Order matters in Quantum Chess. The Queen can split to d3 and c4, but it can also split to c4 and d3. These subtly different moves can yield different underlying phase structures (given their implementation via a square-root iSWAP gate between the source square and the first target, followed by an iSWAP gate between the source and the second target), potentially changing how interference works on, say, a future merge move. So you get 27*26 = 702 possible moves! And that doesn’t include possible merge moves, which might add another 15-20 branches to each node of our tree. 

Do the math and we see that there are roughly 30 times as many moves in Quantum Chess for that queen. Even if we assume the branching factor is only 100, by ply 4 we have 100 million moves to search. We obviously need strong heuristics to do some very aggressive pruning. 

But where do we get strong heuristics for a new game? We don’t have centuries of play to study and determine which sequences of moves are good and which aren’t. This brings us to our first attempt at a Quantum Chess AI. Enter StoQfish.

StoQfish

Quantum Chess is based on chess (in fact, you can play regular Chess all the way through if you and your opponent decide to make no quantum moves), which means that chess skill matters. Could we make a strong chess engine work as a quantum chess AI? Stockfish is open source, and incredibly strong, so we started there.

Given the nature of quantum states, the first thing you think about when you try to adapt a classical strategy into a quantum one, is to split the quantum superposition underlying the state of the game into a series of classical states and then sample them according to their (squared) amplitude in the superposition. And that is exactly what we did. We used the Quantum Chess Engine to generate several chess boards by sampling the current state of the game, which can be thought of as a quantum superposition of classical chess configurations, according to the underlying probability distribution. We then passed these boards to Stockfish. Stockfish would, in theory, return its own weighted distribution of the best classical moves. We had some ideas on how to derive split moves from this distribution, but let’s not get ahead of ourselves.

This approach had limited success and significant failures. Stockfish is highly optimized for classical chess, which means that there are some positions that it cannot process. For example, consider the scenario where a King is in superposition of being captured and not captured; upon capture of one of these Kings, samples taken after such a move will produce boards without a King! Similarly, what if a King in superposition is in check, but you’re not worried because the other half of the King is well protected, so you don’t move to protect it? The concept of check is a problem all around, because Quantum Chess doesn’t recognize it. Things like moving “through check” are completely fine.

You can imagine then why whenever Stockfish encounters a board without a King it crashes. In classical Chess, there is always a King on the board. In Quantum Chess, the King is somewhere in the chess multiverse, but not necessarily in every board returned by the sampling procedure. 

You might wonder if we couldn’t just throw away boards that weren’t valid. That’s one strategy, but we’re sampling probabilities so if we throw out some of the data, then we introduce bias into the calculation, which leads to poor outcomes overall.

We tried to introduce a King onto boards where he was missing, but that became its own computational problem: how do you reintroduce the King in a way that doesn’t change the assessment of the position?

We even tried to hack Stockfish to abandon its obsession with the King, but that caused a cascade of other failures, and tracing through the Stockfish codebase became a problem that wasn’t likely to yield a good result.

This approach wasn’t working, but we weren’t done with Stockfish just yet. Instead of asking Stockfish for the next best move given a position, we tried asking Stockfish to evaluate a position. The idea was that we could use the board evaluations in our own Minimax algorithm. However, we ran into similar problems, including the illegal position problem.

So we decided to try writing our own minimax search, with our own evaluation heuristics. The basics are simple enough. A board’s value is related to the value of the pieces on the board and their location. And we could borrow from Stockfish’s heuristics as we saw fit. 

This gave us Hal 9000. We were sure we’d finally mastered quantum AI. Right? Find out what happened, in the next post.

What does it mean to create a topological qubit?

I’ve worked on topological quantum computation, one of Alexei Kitaev’s brilliant innovations, for around 15 years now.  It’s hard to find a more beautiful physics problem, combining spectacular quantum phenomena (non-Abelian anyons) with the promise of transformative technological advances (inherently fault-tolerant quantum computing hardware).  Problems offering that sort of combination originally inspired me to explore quantum matter as a graduate student. 

Non-Abelian anyons are emergent particles born within certain exotic phases of matter.  Their utility for quantum information descends from three deeply related defining features:

Nucleating a collection of well-separated non-Abelian anyons within a host platform generates a set of quantum states with the same energy (at least to an excellent approximation).  Local measurements give one essentially no information about which of those quantum states the system populates—i.e., any evidence of what the system is doing is hidden from the observer and, crucially, the environment.  In turn, qubits encoded in that space enjoy intrinsic resilience against local environmental perturbations. Swapping the positions of non-Abelian anyons manipulates the state of the qubits.  Swaps can be enacted either by moving anyons around each other as in a shell game, or by performing a sequence of measurements that yields the same effect.  Exquisitely precise qubit operations follow depending only on which pairs the user swaps and in what order.  Properties (1) and (2) together imply that non-Abelian anyons offer a pathway both to fault-tolerant storage and manipulation of quantum information. A pair of non-Abelian anyons brought together can “fuse” into multiple different kinds of particles, for instance a boson or a fermion.  Detecting the outcome of such a fusion process provides a method for reading out the qubit states that are otherwise hidden when all the anyons are mutually well-separated.  Alternatively, non-local measurements (e.g., interferometry) can effectively fuse even well-separated anyons, thus also enabling qubit readout. 

I entered the field back in 2009 during the last year of my postdoc.  Topological quantum computing—once confined largely to the quantum Hall realm—was then in the early stages of a renaissance driven by an explosion of new candidate platforms as well as measurement and manipulation schemes that promised to deliver long-sought control over non-Abelian anyons.  The years that followed were phenomenally exciting, with broadly held palpable enthusiasm for near-term prospects not yet tempered by the practical challenges that would eventually rear their head. 

A PhD comics cartoon on non-Abelian anyons from 2014.

In 2018, near the height of my optimism, I gave an informal blackboard talk in which I speculated on a new kind of forthcoming NISQ era defined by the birth of a Noisy Individual Semi-topological Qubit.  To less blatantly rip off John Preskill’s famous acronym, I also—jokingly of course—proposed the alternative nomenclature POST-Q (Piece Of S*** Topological Qubit) era to describe the advent of such a device.  The rationale behind those playfully sardonic labels is that the inaugural topological qubit would almost certainly be far from ideal, just as the original transistor appears shockingly crude when compared to modern electronics.  You always have to start somewhere.  But what does it mean to actually create a topological qubit, and how do you tell that you’ve succeeded—especially given likely POST-Q-era performance?

To my knowledge those questions admit no widely accepted answers, despite implications for both quantum science and society.  I would like to propose defining an elementary topological qubit as follows:

A device that leverages non-Abelian anyons to demonstrably encode and manipulate a single qubit in a topologically protected fashion. 

Some of the above words warrant elaboration.  As alluded to above, non-Abelian anyons can passively encode quantum information—a capability that by itself furnishes a quantum memory.  That’s the “encode” part.  The “manipulate” criterion additionally entails exploiting another aspect of what makes non-Abelian anyons special—their behavior under swaps—to enact gate operations.  Both the encoding and manipulation should benefit from intrinsic fault-tolerance, hence the “topologically protected fashion” qualifier.  And very importantly, these features should be “demonstrably” verified.  For instance, creating a device hosting the requisite number of anyons needed to define a qubit does not guarantee the all-important property of topological protection.  Hurdles can still arise, among them: if the anyons are not sufficiently well-separated, then the qubit states will lack the coveted immunity from environmental perturbations; thermal and/or non-equilibrium effects might still induce significant errors (e.g., by exciting the system into other unwanted states); and measurements—for readout and possibly also manipulation—may lack the fidelity required to fruitfully exploit topological protection even if present in the qubit states themselves. 

The preceding discussion raises a natural follow-up question: How do you verify topological protection in practice?  One way forward involves probing qubit lifetimes, and fidelities of gates resulting from anyon swaps, upon varying some global control knob like magnetic field or gate voltage.  As the system moves deeper into the phase of matter hosting non-Abelian anyons, both the lifetime and gate fidelities ought to improve dramatically—reflecting the onset of bona fide topological protection.  First-generation “semi-topological” devices will probably fare modestly at best, though one can at least hope to recover general trends in line with this expectation. 

By the above proposed definition, which I contend is stringent yet reasonable, realization of a topological qubit remains an ongoing effort.  Fortunately the journey to that end offers many significant science and engineering milestones worth celebrating in their own right.  Examples include:

Platform verification.  This most indirect milestone evidences the formation of a non-Abelian phase of matter through (thermal or charge) Hall conductance measurements, detection of some anticipated quantum phase transition, etc. 

Detection of non-Abelian anyons. This step could involve conductance, heat capacity, magnetization, or other types of measurements designed to support the emergence of either individual anyons or a collection of anyons.  Notably, such techniques need not reveal the precise quantum state encoded by the anyons—which presents a subtler challenge. 

Establishing readout capabilities. Here one would demonstrate experimental techniques, interferometry for example, that in principle can address that key challenge of quantum state readout, even if not directly applied yet to a system hosting non-Abelian anyons. 

Fusion protocols.  Readout capabilities open the door to more direct tests of the hallmark behavior predicted for a putative topological qubit.  One fascinating experiment involves protocols that directly test non-Abelian anyon fusion properties.  Successful implementation would solidify readout capabilities applied to an actual candidate topological qubit device. 

Probing qubit lifetimes.  Fusion protocols further pave the way to measuring the qubit coherence times, e.g., 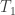and 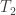—addressing directly the extent of topological protection of the states generated by non-Abelian anyons.  Behavior clearly conforming to the trends highlighted above could certify the device as a topological quantum memory.  (Personally, I most anxiously await this milestone.)

Fault-tolerant gates from anyon swaps.  Likely the most advanced milestone, successfully implementing anyon swaps, again with appropriate trends in gate fidelity, would establish the final component of an elementary topological qubit. 

Most experiments to date focus on the first two items above, platform verification and anyon detection.  Microsoft’s recent Nature paper, together with the simultaneous announcement of supplementary new results, combine efforts in those areas with experiments aiming to establish interferometric readout capabilities needed for a topological qubit.  Fusion, (idle) qubit lifetime measurements, and anyon swaps have yet to be demonstrated in any candidate topological quantum computing platform, but at least partially feature in Microsoft’s future roadmap.  It will be fascinating to see how that effort evolves, especially given the aggressive timescales predicted by Microsoft for useful topological quantum hardware.  Public reactions so far range from cautious optimism to ardent skepticism; data will hopefully settle the situation one way or another in the near future.  My own take is that while Microsoft’s progress towards qubit readout is a welcome advance that has value regardless of the nature of the system to which those techniques are currently applied, convincing evidence of topological protection may still be far off. 

In the meantime, I maintain the steadfast conviction that topological qubits are most certainly worth pursuing—in a broad range of platforms.  Non-Abelian quantum Hall states seem resurgent candidates, and should not be discounted.  Moreover, the advent of ultra-pure, highly tunable 2D materials provide new settings in which one can envision engineering non-Abelian anyon devices with complementary advantages (and disadvantages) compared to previously explored settings.  Other less obvious contenders may also rise at some point.  The prospect of discovering new emergent phenomena mitigating the need for quantum error correction warrants continued effort with an open mind.

Lessons in frustration

Assa Auerbach’s course was the most maddening course I’ve ever taken. 

I was a master’s student in the Perimeter Scholars International program at the Perimeter Institute for Theoretical Physics. Perimeter trotted in world experts to lecture about modern physics. Many of the lecturers dazzled us with their pedagogy and research. We grew to know them not only in class and office hours, but also over meals at Perimeter’s Black-Hole Bistro.

Assa hailed from the Technion in Haifa, Israel. He’d written the book—at least, a book—about condensed matter, the physics of materials. He taught us condensed matter, according to some definition of “taught.” 

Assa zipped through course material. He refrained from defining terminology. He used loose, imprecise language that conveys intuition to experts and only to experts. He threw at us the Hubbard model, the Heisenberg model, the Meissner effect, and magnons. If you don’t know what those terms mean, then I empathize. Really.

So I fought Assa like a groom hauling on a horse’s reins. I raised my hand again and again, insisting on clarifications. I shot off questions as quickly as I could invent them, because they were the only barriers slowing him down. He told me they were.

One day, we were studying magnetism. It arises because each atom in a magnet has a magnetic moment, a tiny compass that can angle in any direction. Under certain conditions, atoms’ magnetic moments tend to angle in opposite directions. Sometimes, not all atoms can indulge this tendency, as in the example below.

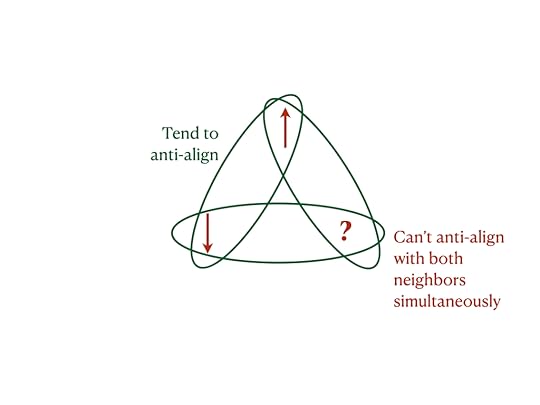
Physicists call this clash frustration, which I wanted to understand comprehensively and abstractly. But Assa wouldn’t define frustration; he’d only sketch an example. 

But what is frustration? I insisted.

It’s when the atoms aren’t happy, he said, like you are now.

After class, I’d escape to the bathroom and focus on breathing. My body felt as though it had been battling an assailant physically. 

Earlier this month, I learned that Assa had passed away suddenly. A former Perimeter classmate reposted the Technion’s news blurb on Facebook. A photo of Assa showed a familiar smile flashing beneath curly salt-and-pepper hair.

Am I defaming the deceased? No. The news of Assa’s passing walloped me as hard as any lecture of his did. I liked Assa and respected him; he was a researcher’s researcher. And I liked Assa for liking me for fighting to learn.

Photo courtesy of the Technion

One day, at the Bistro, Assa explained why the class had leaped away from the foundations of condensed matter into advanced topics so quickly: earlier discoveries felt “stale” to him. Everyone, he believed, could smell their moldiness. I disagreed, although I didn’t say so: decades-old discoveries qualify as new to anyone learning about them for the first time. Besides, 17th-century mechanics and 19th-century thermodynamics soothe my soul. But I respected Assa’s enthusiasm for the cutting-edge. And I did chat with him at the Bistro, where his friendliness shone like that smile.

Five years later, I was sojourning at the Kavli Institute for Theoretical Physics (KITP) in Santa Barbara, near the end of my PhD. The KITP, like Perimeter, draws theorists from across the globe. I spotted Assa among them and reached out about catching up. We discussed thermodynamics and experiments and travel. 

Assa confessed that, at Perimeter, he’d been lecturing to himself—presenting lectures that he’d have enjoyed hearing, rather than lectures designed for master’s students. He’d appreciated my slowing him down. Once, he explained, he’d guest-lectured at Harvard. Nobody asked questions, so he assumed that the students must have known the material already, that he must have been boring them. So he sped up. Nobody said anything, so he sped up further. At the end, he discovered that nobody had understood any of his material. So he liked having an objector keeping him in check.

And where had this objector ended up? In a PhD program and at a mecca for theoretical physicists. Pursuing the cutting edge, a budding researcher’s researcher. I’d angled in the same direction as my former teacher. And one Perimeter classmate, a faculty member specializing in condensed matter today, waxed even more eloquently about Assa’s inspiration when we were students.

Physics needs more scientists like Assa: nose to the wind, energetic, low on arrogance. Someone who’d respond to this story of frustration with that broad smile.

Ten lessons I learned from John Preskill

Last August, Toronto’s Centre for Quantum Information and Quantum Control (CQIQC) gave me 35 minutes to make fun of John Preskill in public. CQIQC was hosting its biannual conference, also called CQIQC, in Toronto. The conference features the awarding of the John Stewart Bell Prize for fundamental quantum physics. The prize derives its name for the thinker who transformed our understanding of entanglement. John received this year’s Bell Prize for identifying, with collaborators, how we can learn about quantum states from surprisingly few trials and measurements.

The organizers invited three Preskillites to present talks in John’s honor: Hoi-Kwong Lo, who’s helped steer quantum cryptography and communications; Daniel Gottesman, who’s helped lay the foundations of quantum error correction; and me. I believe that one of the most fitting ways to honor John is by sharing the most exciting physics you know of. I shared about quantum thermodynamics for (simple models of) nuclear physics, along with ten lessons I learned from John. You can watch the talk here and check out the paper, recently published in Physical Review Letters, for technicalities.

John has illustrated this lesson by wrestling with the black-hole-information paradox, including alongside Stephen Hawking. Quantum information theory has informed quantum thermodynamics, as Quantum Frontiers regulars know. Quantum thermodynamics is the study of work (coordinated energy that we can harness directly) and heat (the energy of random motion). Systems exchange heat with heat reservoirs—large, fixed-temperature systems. As I draft this blog post, for instance, I’m radiating heat into the frigid air in Montreal Trudeau Airport.

So much for quantum information. How about high-energy physics? I’ll include nuclear physics in the category, as many of my Europeans colleagues do. Much of nuclear physics and condensed matter involves gauge theories. A gauge theory is a model that contains more degrees of freedom than the physics it describes. Similarly, a friend’s description of the CN Tower could last twice as long as necessary, due to redundancies. Electrodynamics—the theory behind light bulbs—is a gauge theory. So is quantum chromodynamics, the theory of the strong force that holds together a nucleus’s constituents.

Every gauge theory obeys Gauss’s law. Gauss’s law interrelates the matter at a site to the gauge field around the site. For example, imagine a positive electric charge in empty space. An electric field—a gauge field—points away from the charge at every spot in space. Imagine a sphere that encloses the charge. How much of the electric field is exiting the sphere? The answer depends on the amount of charge inside, according to Gauss’s law.

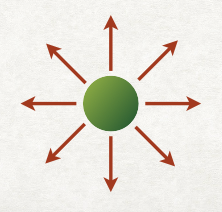
Gauss’s law interrelates the matter at a site with the gauge field nearby…which is related to the matter at the next site…which is related to the gauge field farther away. So everything depends on everything else. So we can’t easily claim that over here are independent degrees of freedom that form a system of interest, while over there are independent degrees of freedom that form a heat reservoir. So how can we define the heat and work exchanged within a lattice gauge theory? If we can’t, we should start biting our nails: thermodynamics is the queen of the physical theories, a metatheory expected to govern all other theories. But how can we define the quantum thermodynamics of lattice gauge theories? My colleague Zohreh Davoudi and her group asked me this question.

I had the pleasure of addressing the question with five present and recent Marylanders…

…the mention of whom in my CQIQC talk invited…

I’m a millennial; social media took off with my generation. But I enjoy saying that my PhD advisor enjoys far more popularity on social media than I do.

How did we begin establishing a quantum thermodynamics for lattice gauge theories?

Someone who had a better idea than I, when I embarked upon this project, was my colleague Chris Jarzynski. So did Dvira Segal, a University of Toronto chemist and CQIQC’s director. So did everyone else who’d helped develop the toolkit of strong-coupling thermodynamics. I’d only heard of the toolkit, but I thought it sounded useful for lattice gauge theories, so I invited Chris to my conversations with Zohreh’s group.

I didn’t create this image for my talk, believe it or not. The picture already existed on the Internet, courtesy of this blog.

Strong-coupling thermodynamics concerns systems that interact strongly with reservoirs. System–reservoir interactions are weak, or encode little energy, throughout much of thermodynamics. For example, I exchange little energy with Montreal Trudeau’s air, relative to the amount of energy inside me. The reason is, I exchange energy only through my skin. My skin forms a small fraction of me because it forms my surface. My surface is much smaller than my volume, which is proportional to the energy inside me. So I couple to Montreal Trudeau’s air weakly.

My surface would be comparable to my volume if I were extremely small—say, a quantum particle. My interaction with the air would encode loads of energy—an amount comparable to the amount inside me. Should we count that interaction energy as part of my energy or as part of the air’s energy? Could we even say that I existed, and had a well-defined form, independently of that interaction energy? Strong-coupling thermodynamics provides a framework for answering these questions.

Kevin Kuns, a former Quantum Frontiers blogger, described how John explains physics through simple concepts, like a ball attached to a spring. John’s gentle, soothing voice resembles a snake charmer’s, Kevin wrote. John charms his listeners into returning to their textbooks and brushing up on basic physics.

Little is more basic than the first law of thermodynamics, synopsized as energy conservation. The first law governs how much a system’s internal energy changes during any process. The energy change equals the heat absorbed, plus the work absorbed, by the system. Every formulation of thermodynamics should obey the first law—including strong-coupling thermodynamics. 

Which lattice-gauge-theory processes should we study, armed with the toolkit of strong-coupling thermodynamics? My collaborators and I implicitly followed

and

We don’t want to irritate experimentalists by asking them to run difficult protocols. Tom Rosenbaum, on the left of the previous photograph, is a quantum experimentalist. He’s also the president of Caltech, so John has multiple reasons to want not to irritate him.

Quantum experimentalists have run quench protocols on many quantum simulators, or special-purpose quantum computers. During a quench protocol, one changes a feature of the system quickly. For example, many quantum systems consist of particles hopping across a landscape of hills and valleys. One might flatten a hill during a quench.

We focused on a three-step quench protocol: (1) Set the system up in its initial landscape. (2) Quickly change the landscape within a small region. (3) Let the system evolve under its natural dynamics for a long time. Step 2 should cost work. How can we define the amount of work performed? By following

John wrote a blog post about how the typical physicist is a one-trick pony: they know one narrow subject deeply. John prefers to know two subjects. He can apply insights from one field to the other. A two-trick pony can show that Gauss’s law behaves like a strong interaction—that lattice gauge theories are strongly coupled thermodynamic systems. Using strong-coupling thermodynamics, the two-trick pony can define the work (and heat) exchanged within a lattice gauge theory. 

An experimentalist can easily measure the amount of work performed,1 we expect, for two reasons. First, the experimentalist need measure only the small region where the landscape changed. Measuring the whole system would be tricky, because it’s so large and it can contain many particles. But an experimentalist can control the small region. Second, we proved an equation that should facilitate experimental measurements. The equation interrelates the work performed1 with a quantity that seems experimentally accessible.

My team applied our work definition to a lattice gauge theory in one spatial dimension—a theory restricted to living on a line, like a caterpillar on a thin rope. You can think of the matter as 2 and the gauge field as more qubits. The system looks identical if you flip it upside-down; that is, the theory has a 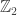symmetry. The system has two phases, analogous to the liquid and ice phases of HO. Which phase the system occupies depends on the chemical potential—the average amount of energy needed to add a particle to the system (while the system’s entropy, its volume, and more remain constant).

My coauthor Connor simulated the system numerically, calculating its behavior on a classical computer. During the simulated quench process, the system began in one phase (like HO beginning as water). The quench steered the system around within the phase (as though changing the water’s temperature) or across the phase transition (as though freezing the water). Connor computed the work performed during the quench.1 The amount of work changed dramatically when the quench started steering the system across the phase transition. 

Not only could we define the work exchanged within a lattice gauge theory, using strong-coupling quantum thermodynamics. Also, that work signaled a phase transition—a large-scale, qualitative behavior.

What future do my collaborators and I dream of for our work? First, we want for an experimentalist to measure the work1 spent on a lattice-gauge-theory system in a quantum simulation. Second, we should expand our definitions of quantum work and heat beyond sudden-quench processes. How much work and heat do particles exchange while scattering in particle accelerators, for instance? Third, we hope to identify other phase transitions and macroscopic phenomena using our work and heat definitions. Fourth—most broadly—we want to establish a quantum thermodynamics for lattice gauge theories.

Five years ago, I didn’t expect to be collaborating on lattice gauge theories inspired by nuclear physics. But this work is some of the most exciting I can think of to do. I hope you think it exciting, too. And, more importantly, I hope John thought it exciting in Toronto.

I was a student at Caltech during “One Entangled Evening,” the campus-wide celebration of Richard Feynman’s 100th birthday. So I watched John sing and dance onstage, exhibiting no fear of embarrassing himself. That observation seemed like an appropriate note on which to finish with my slides…and invite questions from the audience.

Congratulations on your Bell Prize, John.

1Really, the dissipated work.

2Really, hardcore bosons.

Finding Ed Jaynes’s ghost

You might have heard of the conundrum “What do you give the man who has everything?” I discovered a variation on it last October: how do you celebrate the man who studied (nearly) everything? Physicist Edwin Thompson Jaynes impacted disciplines from quantum information theory to biomedical imaging. I almost wrote “theoretical physicist,” instead of “physicist,” but a colleague insisted that Jaynes had a knack for electronics and helped design experiments, too. Jaynes worked at Washington University in St. Louis (WashU) from 1960 to 1992. I’d last visited the university in 2018, as a newly minted postdoc collaborating with WashU experimentalist Kater Murch. I’d scoured the campus for traces of Jaynes like a pilgrim seeking a saint’s forelock or humerus. The blog post “Chasing Ed Jaynes’s ghost” documents that hunt.

I found his ghost this October.

Kater and colleagues hosted the Jaynes Centennial Symposium on a brilliant autumn day when the campus’s trees were still contemplating shedding their leaves. The agenda featured researchers from across the sciences and engineering. We described how Jaynes’s legacy has informed 21st-century developments in quantum information theory, thermodynamics, biophysics, sensing, and computation. I spoke about quantum thermodynamics and information theory—specifically, incompatible conserved quantities, about which my research-group members and I have blogged many times.

Irfan Siddiqi spoke about quantum technologies. An experimentalist at the University of California, Berkeley, Irfan featured on Quantum Frontiers seven years ago. His lab specializes in superconducting qubits, tiny circuits in which current can flow forever, without dissipating. How can we measure a superconducting qubit? We stick the qubit in a box. Light bounces back and forth across the box. The light interacts with the qubit while traversing it, in accordance with the Jaynes–Cummings model. We can’t seal any box perfectly, so some light will leak out. That light carries off information about the qubit. We can capture the light using a photodetector to infer about the qubit’s state.

The first half of Jaynes–Cummings

Bill Bialek, too, spoke about inference. But Bill is a Princeton biophysicist, so fruit flies preoccupy him more than qubits do. A fruit fly metamorphoses from a maggot that hatches from an egg. As the maggot develops, its cells differentiate: some form a head, some form a tail, and so on. Yet all the cells contain the same genetic information. How can a head ever emerge, to differ from a tail? 

A fruit-fly mother, Bill revealed, injects molecules into an egg at certain locations. These molecules diffuse across the egg, triggering the synthesis of more molecules. The knock-on molecules’ concentrations can vary strongly across the egg: a maggot’s head cells contain molecules at certain concentrations, and the tail cells contain the same molecules at other concentrations.

At this point in Bill’s story, I was ready to take my hat off to biophysicists for answering the question above, which I’ll rephrase here: if we find that a certain cell belongs to a maggot’s tail, why does the cell belong to the tail? But I enjoyed even more how Bill turned the question on its head (pun perhaps intended): imagine that you’re a maggot cell. How can you tell where in the maggot you are, to ascertain how to differentiate? Nature asks this question (loosely speaking), whereas human observers ask Bill’s first question.

To answer the second question, Bill recalled which information a cell accesses. Suppose you know four molecules’ concentrations: , , , and . How accurately can you predict the cell’s location? That is, what probability does the cell have of sitting at some particular site, conditioned on the s? That probability is large only at one site, biophysicists have found empirically. So a cell can accurately infer its position from its molecules’ concentrations.

I’m no biophysicist (despite minor evidence to the contrary), but I enjoyed Bill’s story as I enjoyed Irfan’s. Probabilities, information, and inference are abstract notions; yet they impact physical reality, from insects to quantum science. This tension between abstraction and concreteness arrested me when I first encountered entropy, in a ninth-grade biology lecture. The tension drew me into information theory and thermodynamics. These toolkits permeate biophysics as they permeate my disciplines. So, throughout the symposium, I spoke with engineers, medical-school researchers, biophysicists, thermodynamicists, and quantum scientists. They all struck me as my kind of people, despite our distribution across the intellectual landscape. Jaynes reasoned about distributions—probability distributions—and I expect he’d have approved of this one. The man who studied nearly everything deserves a celebration that illuminates nearly everything.

Beyond NISQ: The Megaquop Machine

On December 11, I gave a keynote address at the Q2B 2024 Conference in Silicon Valley. This is a transcript of my remarks. The slides I presented are here.

NISQ and beyond

I’m honored to be back at Q2B for the 8th year in a row.

The Q2B conference theme is “The Roadmap to Quantum Value,” so I’ll begin by showing a slide from last year’s talk. As best we currently understand, the path to economic impact is the road through fault-tolerant quantum computing. And that poses a daunting challenge for our field and for the quantum industry.

We are in the NISQ era. And NISQ technology already has noteworthy scientific value. But as of now there is no proposed application of NISQ computing with commercial value for which quantum advantage has been demonstrated when compared to the best classical hardware running the best algorithms for solving the same problems. Furthermore, currently there are no persuasive theoretical arguments indicating that commercially viable applications will be found that do not use quantum error-correcting codes and fault-tolerant quantum computing.

NISQ, meaning Noisy Intermediate-Scale Quantum, is a deliberately vague term. By design, it has no precise quantitative meaning, but it is intended to convey an idea: We now have quantum machines such that brute force simulation of what the quantum machine does is well beyond the reach of our most powerful existing conventional computers. But these machines are not error-corrected, and noise severely limits their computational power.

In the future we can envision FASQ* machines, Fault-Tolerant Application-Scale Quantum computers that can run a wide variety of useful applications, but that is still a rather distant goal. What term captures the path along the road from NISQ to FASQ? Various terms retaining the ISQ format of NISQ have been proposed [here, here, here], but I would prefer to leave ISQ behind as we move forward, so I’ll speak instead of a megaquop or gigaquop machine and so on meaning one capable of executing a million or a billion quantum operations, but with the understanding that mega means not precisely a million but somewhere in the vicinity of a million.

Naively, a megaquop machine would have an error rate per logical gate of order 10^{-6}, which we don’t expect to achieve anytime soon without using error correction and fault-tolerant operation. Or maybe the logical error rate could be somewhat larger, as we expect to be able to boost the simulable circuit volume using various error mitigation techniques in the megaquop era just as we do in the NISQ era. Importantly, the megaquop machine would be capable of achieving some tasks beyond the reach of classical, NISQ, or analog quantum devices, for example by executing circuits with of order 100 logical qubits and circuit depth of order 10,000.

What resources are needed to operate it? That depends on many things, but a rough guess is that tens of thousands of high-quality physical qubits could suffice. When will we have it? I don’t know, but if it happens in just a few years a likely modality is Rydberg atoms in optical tweezers, assuming they continue to advance in both scale and performance.

What will we do with it? I don’t know, but as a scientist I expect we can learn valuable lessons by simulating the dynamics of many-qubit systems on megaquop machines. Will there be applications that are commercially viable as well as scientifically instructive? That I can’t promise you.

The road to fault tolerance

To proceed along the road to fault tolerance, what must we achieve? We would like to see many successive rounds of accurate error syndrome measurement such that when the syndromes are decoded the error rate per measurement cycle drops sharply as the code increases in size. Furthermore, we want to decode rapidly, as will be needed to execute universal gates on protected quantum information. Indeed, we will want the logical gates to have much higher fidelity than physical gates, and for the logical gate fidelities to improve sharply as codes increase in size. We want to do all this at an acceptable overhead cost in both the number of physical qubits and the number of physical gates. And speed matters — the time on the wall clock for executing a logical gate should be as short as possible.

A snapshot of the state of the art comes from the Google Quantum AI team. Their recently introduced Willow superconducting processor has improved transmon lifetimes, measurement errors, and leakage correction compared to its predecessor Sycamore. With it they can perform millions of rounds of surface-code error syndrome measurement with good stability, each round lasting about a microsecond. Most notably, they find that the logical error rate per measurement round improves by a factor of 2 (a factor they call Lambda) when the code distance increases from 3 to 5 and again from 5 to 7, indicating that further improvements should be achievable by scaling the device further. They performed accurate real-time decoding for the distance 3 and 5 codes. To further explore the performance of the device they also studied the repetition code, which corrects only bit flips, out to a much larger code distance. As the hardware continues to advance we hope to see larger values of Lambda for the surface code, larger codes achieving much lower error rates, and eventually not just quantum memory but also logical two-qubit gates with much improved fidelity compared to the fidelity of physical gates.

Last year I expressed concern about the potential vulnerability of superconducting quantum processors to ionizing radiation such as cosmic ray muons. In these events, errors occur in many qubits at once, too many errors for the error-correcting code to fend off. I speculated that we might want to operate a superconducting processor deep underground to suppress the muon flux, or to use less efficient codes that protect against such error bursts.

The good news is that the Google team has demonstrated that so-called gap engineering of the qubits can reduce the frequency of such error bursts by orders of magnitude. In their studies of the repetition code they found that, in the gap-engineered Willow processor, error bursts occurred about once per hour, as opposed to once every ten seconds in their earlier hardware.  Whether suppression of error bursts via gap engineering will suffice for running deep quantum circuits in the future is not certain, but this progress is encouraging. And by the way, the origin of the error bursts seen every hour or so is not yet clearly understood, which reminds us that not only in superconducting processors but in other modalities as well we are likely to encounter mysterious and highly deleterious rare events that will need to be understood and mitigated.

Real-time decoding

Fast real-time decoding of error syndromes is important because when performing universal error-corrected computation we must frequently measure encoded blocks and then perform subsequent operations conditioned on the measurement outcomes. If it takes too long to decode the measurement outcomes, that will slow down the logical clock speed. That may be a more serious problem for superconducting circuits than for other hardware modalities where gates can be orders of magnitude slower.

For distance 5, Google achieves a latency, meaning the time from when data from the final round of syndrome measurement is received by the decoder until the decoder returns its result, of about 63 microseconds on average. In addition, it takes about another 10 microseconds for the data to be transmitted via Ethernet from the measurement device to the decoding workstation. That’s not bad, but considering that each round of syndrome measurement takes only a microsecond, faster would be preferable, and the decoding task becomes harder as the code grows in size.

Riverlane and Rigetti have demonstrated in small experiments that the decoding latency can be reduced by running the decoding algorithm on FPGAs rather than CPUs, and by integrating the decoder into the control stack to reduce communication time. Adopting such methods may become increasingly important as we scale further. Google DeepMind has shown that a decoder trained by reinforcement learning can achieve a lower logical error rate than a decoder constructed by humans, but it’s unclear whether that will work at scale because the cost of training rises steeply with code distance. Also, the Harvard / QuEra team has emphasized that performing correlated decoding across multiple code blocks can reduce the depth of fault-tolerant constructions, but this also increases the complexity of decoding, raising concern about whether such a scheme will be scalable.

Trading simplicity for performance

The Google processors use transmon qubits, as do superconducting processors from IBM and various other companies and research groups. Transmons are the simplest superconducting qubits and their quality has improved steadily; we can expect further improvement with advances in materials and fabrication. But a logical qubit with very low error rate surely will be a complicated object due to the hefty overhead cost of quantum error correction. Perhaps it is worthwhile to fashion a more complicated physical qubit if the resulting gain in performance might actually simplify the operation of a fault-tolerant quantum computer in the megaquop regime or well beyond. Several versions of this strategy are being pursued.

One approach uses cat qubits, in which the encoded 0 and 1 are coherent states of a microwave resonator, well separated in phase space, such that the noise afflicting the qubit is highly biased. Bit flips are exponentially suppressed as the mean photon number of the resonator increases, while the error rate for phase flips induced by loss from the resonator increases only linearly with the photon number. This year the AWS team built a repetition code to correct phase errors for cat qubits that are passively protected against bit flips, and showed that increasing the distance of the repetition code from 3 to 5 slightly improves the logical error rate. (See also here.)

Another helpful insight is that error correction can be more effective if we know when and where the errors occur in a quantum circuit. We can apply this idea using a dual rail encoding of the qubits. With two microwave resonators, for example, we can encode a qubit by placing a single photon in either the first resonator (the 10) state, or the second resonator (the 01 state). The dominant error is loss of a photon, causing either the 01 or 10 state to decay to 00. One can check whether the state is 00, detecting whether the error occurred without disturbing a coherent superposition of 01 and 10. In a device built by the Yale / QCI team, loss errors are detected over 99% of the time and all undetected errors are relatively rare. Similar results were reported by the AWS team, encoding a dual-rail qubit in a pair of transmons instead of resonators.

Another idea is encoding a finite-dimensional quantum system in a state of a resonator that is highly squeezed in two complementary quadratures, a so-called GKP encoding. This year the Yale group used this scheme to encode 3-dimensional and 4-dimensional systems with decay rate better by a factor of 1.8 than the rate of photon loss from the resonator. (See also here.)

A fluxonium qubit is more complicated than a transmon in that it requires a large inductance which is achieved with an array of Josephson junctions, but it has the advantage of larger anharmonicity, which has enabled two-qubit gates with better than three 9s of fidelity, as the MIT team has shown.

Whether this trading of simplicity for performance in superconducting qubits will ultimately be advantageous for scaling to large systems is still unclear. But it’s appropriate to explore such alternatives which might pay off in the long run.

Error correction with atomic qubits

We have also seen progress on error correction this year with atomic qubits, both in ion traps and optical tweezer arrays. In these platforms qubits are movable, making it possible to apply two-qubit gates to any pair of qubits in the device. This opens the opportunity to use more efficient coding schemes, and in fact logical circuits are now being executed on these platforms. The Harvard / MIT / QuEra team sampled circuits with 48 logical qubits on a 280-qubit device –- that big news broke during last year’s Q2B conference. Atom computing and Microsoft ran an algorithm with 28 logical qubits on a 256-qubit device. Quantinuum and Microsoft prepared entangled states of 12 logical qubits on a 56-qubit device.

However, so far in these devices it has not been possible to perform more than a few rounds of error syndrome measurement, and the results rely on error detection and postselection. That is, circuit runs are discarded when errors are detected, a scheme that won’t scale to large circuits. Efforts to address these drawbacks are in progress. Another concern is that the atomic movement slows the logical cycle time. If all-to-all coupling enabled by atomic movement is to be used in much deeper circuits, it will be important to speed up the movement quite a lot.

Toward the megaquop machine

How can we reach the megaquop regime? More efficient quantum codes like those recently discovered by the IBM team might help. These require geometrically nonlocal connectivity and are therefore better suited for Rydberg optical tweezer arrays than superconducting processors, at least for now. Error mitigation strategies tailored for logical circuits, like those pursued by Qedma, might help by boosting the circuit volume that can be simulated beyond what one would naively expect based on the logical error rate. Recent advances from the Google team, which reduce the overhead cost of logical gates, might also be helpful.

What about applications? Impactful applications to chemistry typically require rather deep circuits so are likely to be out of reach for a while yet, but applications to materials science provide a more tempting target in the near term. Taking advantage of symmetries and various circuit optimizations like the ones Phasecraft has achieved, we might start seeing informative results in the megaquop regime or only slightly beyond.

As a scientist, I’m intrigued by what we might conceivably learn about quantum dynamics far from equilibrium by doing simulations on megaquop machines, particularly in two dimensions. But when seeking quantum advantage in that arena we should bear in mind that classical methods for such simulations are also advancing impressively, including in the past year (for example, here and here).

To summarize, advances in hardware, control, algorithms, error correction, error mitigation, etc. are bringing us closer to megaquop machines, raising a compelling question for our community: What are the potential uses for these machines? Progress will require innovation at all levels of the stack.  The capabilities of early fault-tolerant quantum processors will guide application development, and our vision of potential applications will guide technological progress. Advances in both basic science and systems engineering are needed. These are still the early days of quantum computing technology, but our experience with megaquop machines will guide the way to gigaquops, teraquops, and beyond and hence to widely impactful quantum value that benefits the world.

I thank Dorit Aharonov, Sergio Boixo, Earl Campbell, Roland Farrell, Ashley Montanaro, Mike Newman, Will Oliver, Chris Pattison, Rob Schoelkopf, and Qian Xu for helpful comments.

*The acronym FASQ was suggested to me by Andrew Landahl.

The megaquop machine (image generated by ChatGPT).