Book Note: Tony Roy, Symbolic Logic, #2

To continue, then, with the comments on Tony Roy’s  Symbolic Logic: An Accessible Introduction to Serious Mathematical Logic,  Part II is called “Transition: Reasoning about Logic”, and is almost another 100 pages, though it consists of just two chapters.

Chapter 7 is a curious affair. It’s called “Direct Semantic Reasoning”, and the aim is to get the student to be able to use their understanding of the official semantics to demonstrate that, e.g., (i) 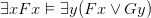or more challengingly (ii) 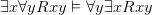, while also being able to show e.g. (iii) . And yes, we of course want students to be able to do these things. Or rather more carefully, we want a student to able to produce informal but rigorous proofs of entailments given the definition of semantic consequence, and to produce counterexamples to witness non-entailments. This amounts to learning how to do some bits of (pretty elementary) mathematical reasoning, and students coming from a non-maths background need to be given some exemplars and models of this sort of informal reasoning done with the right amount of detail to pass muster.

But Roy is keen to replace informal proofs with formal derivations set out in natural deduction style, and the results seem to me to be rebarbative and consequently unhelpful. It is difficult to believe that students will find their abilities at informal reasoning actually improved by the sort of messy regimentations we find in this chapter. Have  a look at p. 364 and ask if this is likely to help a student who doesn’t immediately see why, morally, (ii) should be true.

In his Preface, Roy tries to make a case for his approach in this chapter, but I’m not convinced. And to the extent that the idea is to give students an example of  working formally in reasoning about logic, then we have to hand a framework for formalizing semantic reasoning which is much, much more elegant — i.e. use semantic tableaux, which are designed for the job!

Chapter 8 is on Mathematical Induction. This starts with a general discussion of induction, with some simple arithmetical and geometrical examples. Roy then goes on to give some applications of induction to prove syntactic and semantic facts about his formal languages. The chapter seems  pretty clear, though as before things are perhaps rather stretched out. However,  philosophy students needing to get their heads round the idea of induction and struggling with brisker presentations could very well find this a useful compendium.

To be continued.