Does mathematics need a philosophy? — 1
At last week’s meeting of the Trinity Mathematical Society, Imre Leader and Thomas Forster gave introductory talks on “Does Mathematics need a Philosophy?” to a startlingly large audience, before a question-and-answer session. The topic is quite a big one, and the talks were very short. But here are a few after-thoughts (primarily for members of TMS, but others might be interested …).
(1) Imre did very briskly sketch a couple of recognizably philosophical views about mathematics, platonism and formalism. And he suggested that mathematicians tend to be platonist in their assumptions about what they are up to (in so far as they think they are exploring a determinate abstract mathematical universe, where there are objective truths to be discovered) but they turn formalist when writing up their proofs for public consumption. But I think that runs together formalism as an account of the nature of mathematics (“it’s all juggling with meaningless symbols, a game of seeing what symbol strings you can ‘deduce’ from other strings according to given rules”) with the project of formalization. Since I’ve more than once heard other mathematicians just make the same conflation, it’s worth pausing to pick it apart. (If some of the following sounds familiar, it is because I’m shamelessly plagiarizing my earlier self.)
To be sure, then, in presenting complex mathematical arguments, it helps to regiment our propositions into mathematical-English-plus-notation in ways which are expressly designed to be precise, free from obscurities, and where the logical structure of our claims is clear [think of the way we use the quantifier/variable notation -- as in 
— to make the structure of statements of generality crystal clear]. Then we try to assemble our propositions into something approximating to a chain of formal deductions. Why? Because this enforces honesty: we have to keep a tally of the premisses we invoke, and of exactly what inferential moves we are using. And honesty is the best policy. Suppose we get from the given premisses to some target conclusion by inference steps each one of which is obviously valid (no suppressed premisses are smuggled in, and there are no suspect inferential moves). Then our honest toil then buys us the right to confidence that our premisses really do entail the desired conclusion. Hooray!
True, even the most tough-minded mathematics texts are written in an informal mix of ordinary language and mathematical symbolism. Proofs are very rarely spelt out in every formal detail, and so their presentation still falls short of the logicians’ ideal of full formalization. But we will hope that nothing stands in the way of our more informally presented mathematical proofs being sharpened up into fully formalized ones. Indeed, we might hope and pray that they could ideally be set out in a strictly regimented formal language of the kind that logicians describe (and which computer proofs implement), with absolutely every tiny inferential move made totally explicit, so that everything could be mechanically checked as being in accord with some overtly acknowledged rules of inference, with the proofs ultimately starting from our stated axioms.
True, the extra effort of laying out everything in complete detail will almost never be worth the cost in time and ink. In mathematical practice we use enough formalization to convince ourselves that our results don’t depend on illicit smuggled premisses or on dubious inference moves, and leave it at that — our motto is “sufficient unto the day is the rigour thereof”. Here are local heroes Whitehead and Russell making the point in Principia:
Most mathematical investigation is concerned not with the analysis of the complete process of reasoning, but with the presentation of such an abstract of the proof as is sufficient to convince a properly instructed mind.
(A properly instructed mind being, like them, a Trinity mathmo.)
Let’s all agree, then: formalization (at least up to a point) is a Good Thing, because a proof sufficiently close to the formalized ideal is just the thing you need in order to check that your bright ideas really do fly and then to convince the properly instructed minds of your readers. [Well, being a sort-of-philosophical remark, you'll be able to find some philosophers who seem to disagree, as is the way with that cantankerous bunch. But the dissenters are usually just making the point that producing formalizable proofs isn't the be-all and end-all of mathematics -- and we can happily agree with that. For a start, we often hanker after proofs that not only work but are in some way explanatory, whatever exactly that means.]
So Imre would have been dead right if he had said that mathematicians get to work (semi)-formalizing when they check and write up their proofs. But in fact, having described formalism as the game-with-meaningless-symbols idea, he said that mathematicians turn formalist in their proofs. Yet that’s a quite different claim.
Anyone who is tempted to run them together should take a moment to recall that one of the earliest clear advocates of the virtues of formalization was Frege, the original arch anti-formalist. But we don’t need to wheel out the historical heavy guns. The key point to make here is a very simple one. Writing things in a regimented, partially or completely symbolic, language (so that you can better check what follows from what) doesn’t mean that you’ve stopped expressing propositions and started manipulating meaningless symbols. Hand-crafted, purpose-designed languages are still languages. The move from ‘two numbers have the same same sum whichever way round you add them’ to e.g. ‘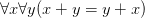
’ changes the medium but not the message. And the fact that you can and should temporally ignore the meaning of non-logical predicates and functions while checking that a formally set-out proof obeys the logical rules [because the logical rules are formal!], doesn’t mean that non-logical predicates and functions don’t have a meaning!
In sum then, the fact that (on their best public behaviour) mathematicians take at least some steps towards making their proofs formally kosher doesn’t mean that they are being (even temporary) formalists.
Which is another Good Thing, because out-right naive formalism of the “it’s all meaningless symbols” variety is a pretty wildly implausible philosophy of mathematics. But that’s another story ….
To be continued
