Map Coloring Revisited

Following the coloring theme from Bill's last post, a few years ago I asked you readers for natural examples of maps that were and were not three colorable. Chris Bogart gave a nice non-trivial example of a three-colorable country, Armenia.













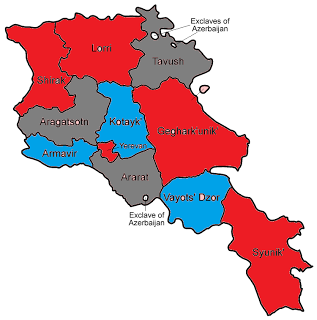
But I also wanted a natural example that was four-colorable even though every interior region had an even number of neighbors. In my book I ended up making up my own fake country map.











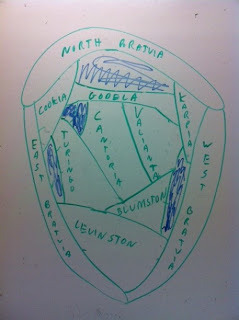
(Sorry for the hand-drawn picture and getting East-West wrong. Looks better in the book)




So once again I'd still like to see a natural example. Here's a simple 7-node graph with every interior node with even degree but not 3-colorable. 









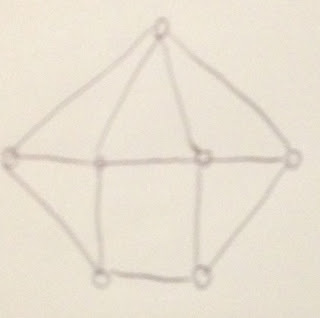
There must be some real world map that captures this graph.




I'll make the same deal I made before, an autographed copy of my book for the best example of a real-world example of a non-three colorable map with interior regions with an even number of neighbors. Should be a real political unit--not just a collection of states.