Yanofsky, Monoidal Category Theory — 3
Some brief comments on Chapters 2 to 4 of Yanofsky’s book, firstly on the main sections of those chapters. In Chapter 2, categories are defined, we meet lots of examples, and then different kinds of arrows are defined, along with subcategories and opposite categories, and a little more. Chapter 3 then treats “structures within categories”, meaning products and coproducts (at some length) and then other limits (more briskly). A quick look at slice and co-slice categories is tacked on the end. Chapter 4 then discusses “relationships between categories”; so we meet functors, natural transformations, adjunctions, Yoneda and more.
These chapters therefore aim to cover a very familiar menu — much the same, for example, as in Tom Leinster’s excellent Basic Category Theory. Yanofksy’s sections take 129 (larger) pages, while Leinster takes 162 (smaller) pages and goes a little further. Now, as I mentioned before, I do like the order in which Yanofksy approaches the material. However — as I already indicated in my first post about Monoidal Category Theory — I do overall considerably prefer Leinster’s treatment. Why? Because it strikes me as more elegant and better motivated. At some key points Leinster’s explanations of particular points are clearer. While his discussions of major themes can usefully be a bit more expansive.
For just one example of a particular point, both authors give only headline versions of a proof that a category with finite products and equalizers has all finite limits. But Yanofsky’s version (p. 109) seems pretty under-described: I doubt that a neophyte will be able to work out a detailed proof. Leinster gives the reader significantly more hints of how to proceed.
For just one example of the treatment of a major theme, you could compare Yanofsky’s six brusque pages around and about Yoneda with Leinster’s more generous and helpful dozen.
And so it goes: examples can be multiplied. Yes, Leinster’s book is “developed out of masters-level courses”, while Yanoksky says in his Preface “we do not assume the reader is already a mathematician”. But in fact, when it gets down to business, I think seriously tackling Yanoksky’s book requires a level of mathematical maturity broadly comparable to what it takes to tackle Leinster’s. So Basic Category Theory still gets my vote for its coverage of the basic menu if you want something at that level. While my Introducing Category Theory (or more specifically, Parts I and III in the currently available version) is freely available if you want a more relaxed and slower-moving treatment of the same topics with more proofs fully spelt out.
But what about the added ‘mini-courses’ which end each of Yanofksy’s chapters? Do these add value? They are a very mixed bag. Chapter 2 adds a sixteen page mini-course on ‘Basic Linear Algebra’: I suspect most readers would either need somewhat less (if just seeking quick reminders for later use) or want significantly more (if this is actually all news to them). Chapter 3 adds thirty pages on ‘Self-Referential Paradoxes’: I’ll return to this in a future post. Then Chapter 4 has a seventeen page mini-course on ‘Basic Categorical Logic’. I’ll here say just a bit more about this last section.
If you are looking for excitements, e.g. an explanation of why the internal logic of a topos is intuitionistic by default, then this isn’t for you! (We don’t meet toposes for another 300 pages). Nor, rather oddly, do we get an elucidation of the Galois connection between syntax and semantics. Rather, Yanofsky is concerned with the elementary points that we can see conjunctions (logical products) as products in the categorial sense, we can see conjunction as left adjoint to implication, and more interestingly there are adjunctions between universal and existential quantification and a certain operation which adds a free variable.
To my mind, Yanofsky makes rather heavy weather of this. And along the way he says a number of things which will annoy logicians. We are told that “the predicate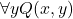 
is true iff …”: predicates aren’t true or false. We are told that a dyadic predicate has a set of pairs as its “domain of discourse”: predicates don’t have domains of discourse. And so on.
Our author ends with wildly over-excited claims for category theory in its applications to baby logic. Thus “We showed that the various logical operations do not stand alone. Category theory shows that the operations are intimately connected to each other and can be defined in terms of each other with universal properties.” It is logic, not category theory, which shows that some familiar logical operations are intimately connected to each other and can be defined in terms of each other: giving a categorial spin adds very little. Again “We showed that many of the truths of propositional and predicate logic are simple consequences of the universal properties of the operations. A logical statement is not true because it seems true [wow, that’s news?!]. Rather, the statement has to be true because of the way that operations are defined in terms of other operations.” But again, that’s just logic for you — nothing to do with category theory.
The post Yanofsky, Monoidal Category Theory — 3 appeared first on Logic Matters.
