Yanofsky, Monoidal Category Theory — 2

I’ll offer some more comments over the next blog post or two on Chapters 1 to 4 of Monoidal Category Theory, the chapters which comprise Yanofsky’s introductory course on core category theory, before we reach the monoidal delights.

Chapter 1, after some short and very introductory sections, is mostly taken up with a 25 page mini-course ‘Sets and Categorical Thinking’. In fact, we not only meet sets and functions, but also graphs and groups and their respective homomorphisms: we get some familiar definitions, and a few results results along the way (such as that a function 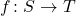is injective iff there is a function 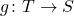such that 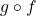equals the identity function on ).

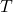We could quibble at various points. For example, having been told that a function is “an assignment of an element of to every element of ”, we are then asked to buy the claim that for any set 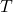there is a function to it from the empty set. The naive reader might reasonably suppose that if has no elements, then there is no assignment of corresponding elements of 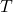to be had. But fussing about this sort of thing would be boring, so let me cut to the chase, to make the main point about Yanofsky’s introductory remarks about sets.

For Yanofksy, a set is a “collection of elements”. And he seems to place no restriction at all on the sorts of things that can be elements of sets. So we have sets whose members are numbers (p. 8), shirts (p. 8), people (p. 11), US states (p. 22), street corners (p. 24), web pages (p. 25), Facebook accounts (p. 25), ideas (p. 115) — as well as more sets. So be it. Yes, there is a debate to be had about whether talking of sets of shirts or people or ideas is more than a convenient façon de parler, a way of talking in the singular about perhaps many things at once, which could be cashed out in an alternative plural idiom without any commitment to new entities over and above the shirts, people or ideas. But that’s not a debate for here. Without getting into ontological wrangles, let’s go along with this sweepingly promiscuous use of ‘set’ (arguably indeed the everyday one) where — whatever your favourite widgets might be — there can be sets of that sort of thing.

So to the obvious question: is this understanding of ‘set’ still in play at the beginning of Chapter 2 where categories are defined, and the first example given is — as so often — “the category 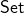” of sets and functions [note the definite article]? So, among the objects of the the category 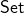, do we find e.g. the set of Yanofsky’s shirts, and — a brand new arrival, with its newly-baked members — today’s set of Mrs Logic Matters’s excellent scones? We are told on p. 37 that “the collection of all sets form a category”, presumably the category 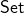(NB the ‘all’).

But I doubt that this is what Yanofsky really intends. As usually construed, “the category 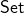” refers not to some fluctuating universe including sets with concrete members which may pop in and out of existence. Rather the objects of 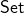are standardly taken to be members of some hierarchy of pure sets (so its sets all the way down) as described by ZFC or some nice extension thereof. Thus, of course, Mac Lane in defining categories as implementations of the axioms of category theory in a universe of pure sets as described by ZFC plus (Categories for the Working Mathematician, pp. 10, 23). Compare Horst Schubert in his terse but very good and clear Categories (§3.1), who writes “One has to be aware that the set theory used here has no “primitive (ur-) elements”; elements of sets, or classes …, are always themselves sets.” Compare too, for example, Borceux in his Handbook of Categorical Algebra I, in his opening pages, or Emily Riehl in her Category Theory in Context, p. 6: “common practice among category theorists is to work in an extension of the usual Zermelo–Fraenkel axioms of set theory, with new axioms allowing one to distinguish between “small” and “large” sets, or between sets and classes” (but to repeat, the ZF axioms describe a universe of pure sets, where Yanofsky’s shirts and Mrs Logic Matters’s scones are not to be found!).

So if Yanofsky’s category 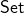really is intended to be some fluctuating universe of sets including sets with concrete ur-elements, then our author should certainly have told us that he is taking a pretty deviant line on what 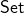comprises as compared with standard texts. But I suspect that there is actually an unacknowledged crashing of the gears between what is being said about sets in Yanofsky’s Chapter 1 and what is being assumed in Chapter 2 onwards once the category 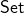officially enters stage left, where the discussion seems to proceed in a conventional way. In which case, Yanofsky’s should have explained carefully the reasons for the radical narrowing of focus which means that 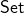doesn’t after all contain many of the sets he has previously been talking about. (Apologies if I have missed the relevant discussion — one of the downsides of working from a physical book is I that can’t double-check with some appropriate text-searches.)

As to the remarks on ‘Categorical Thinking’ in that first mini-course, we get the usual kind of hand-waving remarks about morphisms being “central” in category theory (as if they weren’t all along in the algebra and topology we learnt back when I were a lad), or category theory not being about ‘things’ but about how ‘things’ relate to other ‘things’ (as if telling you about Jack relates to Jill I am not telling you something about Jack?). Sure, the hand-waving is fine in its place, but to my tastes Yanofsky does rather over-do it.

The post Yanofsky, Monoidal Category Theory — 2 appeared first on Logic Matters.