Subriemannian parallel parking on the Heisenberg group

I met Mike Freedman last week at CMSA and I learned a great metaphor about an old favorite subject of mine, random walks on groups.

The Heisenberg group is the group of upper triangular matrices with 1’s on the diagonal:

You can take a walk on the integral or Z/pZ points of the Heisenberg group using the standard generators

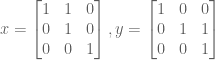
and their inverses. How do you get a central element

with these generators? The way that presents itself most immediately is that the commutator [x,y] is the central element with 1 in the upper right-hand corner. So the matrix above is [x,y]^c, a word of length 4c. But you can do better! If m is an integer of size about 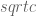, then [x^m, y^m] is central with an m^2 in the upper right-hand corner; then you can multiply by another 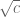or so copies of [x,y] to get the desired element in about 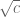steps.

Mike F. likes to think of the continuous version of this walk. This is a funny process; the Heisenberg group over R is a 3-manifold, but you only have two infinitesimal directions in which you’re allowed to move. The cost of moving infinitesimally in the c-direction above is infinite! 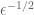(One way of thinking of this: by the above argument, it costs to travel in that direction, but when is close to 0, the cost per unit of distance goes to infinity!

This is what’s called a subriemannian structure. It’s like a Riemannian metric, but in each tangent space there’s a proper subspace in which you’re allowed to move at nonzero speed. But the brackets between things are substantial enough that you can still get anywhere on the manifold, you just have to shimmy a bit.

That was not a very clean definition, and I’m not going to give you one, but I will give you a very useful metaphor Mike explained to me. It’s like parallel parking! The state of your car is described by a point on a three-manifold R^2 x S^1, where the first two coordinates govern the car’s position on the street and the last the direction of the wheels. (OK this is probably an interval in S^1, not the whole S^1, unless you have a very cool car, but set that aside.) And at any point you have the ability to turn the wheels sideways, or you can inch forward or backwards, but you can’t hop the car to the side! So there’s a two-dimensional subspace of the tangent space in which you can move at finite costs. But if you need to move your car two feet in a direction orthogonal to the direction you’re facing — that is, if you need to parallel park — you can do it. You just have to shimmy a bit, where “shimmy” is the parallel parking term for “commutator” — this is really the same thing as [x,y] giving you a positive amount of motion in the infinite-cost direction.