Book note: Kaye, The Mathematics of Logic
Richard Kaye’s The Mathematics of Logic (CUP, 2007) is subtitled ‘A guide to completeness theorems and their application’. This is an unconventional — one might even say idiosyncratic — introduction to first-order-logic and related themes. Some will appreciate it as a somewhat bumpy but illuminating ride: but probably most will prefer a more conventional text for a first encounter with FOL.
There are a dozen chapters, each comprising a main section (which should be accessible to undergraduates), followed by a section of examples and exercises, followed by one or sometimes two optional starred sections which can require more mathematical background (in some cases, graduate level). I’ll return to those optional sections later; but let’s concentrate first on the main sections together with their amplifying sections of examples and exercises. These make for a core book of under 140 pages. So how does the story go?
Ch. 1 is on König’s Lemma (initially for binary trees). Why start here? The idea is that we have two relevant ideas of infinity for such trees, (i) a ‘definition from perfect information’, where we take a god’s eye view of the whole tree and say it is infinite if it has an infinite number of nodes, and (ii) a ‘definition from imperfect information’, where we take the view of, as it were, an ant who can’t see the whole tree but is crawling along a path, who says the tree is infinite if it has an unending path. We then have a ‘soundness’ proof (trivial) and a ‘completeness’ proof (König’s Lemma) which tell us that for binary trees the two definitions of an infinite tree come to the same. Kaye’s suggestion is that this provides an analogue for the soundness and completeness proofs that will concern us later, relating semantic definitions of validity (which are definitions from perfect information, surveying all models) and syntactic definitions (it is enough to have imperfect information, just one particular proof). Or so goes the story.
Ch. 2 is on posets and Zorn’s Lemma. We know that at some point, when it comes to a strong completeness theorem for FOL with an uncountable language we’ll need Zorn’s Lemma or an equivalent. This chapter provides a pretty clear introduction.
Ch. 3 introduces a toy formal system with simple rules for deriving finite binary strings from an initial set of such strings. We get some illustrative syntactic reasoning about what can and can’t be derived by manipulations in the system. And then we meet an interpretation of the formalism in terms of infinite paths in binary trees, and find proofs of corresponding soundness and completeness theorems. Ch. 4 gives us another toy system, this time with a reductio rule (and we get a Fitch-style plan for laying out reductio derivations). This time the associated interpretation is to do with posets. So these two chapters aim to introduce both some proof-theoretic and semantic ideas in particularly simple contexts. These chapters could work rather well for some readers.
Ch. 5 tells us a little about those posets which are lattices and then introduces Boolean algebras.
With those preliminaries in place, we reach the core of the book. First, Ch. 6 introduces (clearly though rather rapidly?) a Fitch-style proof system for propositional logic. And Ch. 7 treats semantics, though — rather unusually — semantic consequence is officially defined from the start in terms of valuations over all Boolean algebras. It is then proved as a result that this notion is equivalent to the usual one defined in terms of two-valued interpretations. (But we miss the usual idea that two-valued interpretation gives the sense of the connectives.)
Ch. 8 is more on the algebraic theory of Boolean algebras, filters and ideals etc.: the main result is the Boolean Prime Ideal Theorem. (Though this chapter probably could/should be skipped on a first reading).
Then we get to FOL. Ch. 9 introduces the language of first-order logic with identity, and gives a Fitch-style proof-system. I think this would all be too quickly done if you’d really never encountered either a careful treatment of the language or a proof system for quantified logic before. There is only an incomplete gesture towards a semantic story too — note in particular this remark:
If an L-formula
has free variables, these variables must be given some meaning or interpretation in an L-structure M before we can say what it means for
. In other words, these free variables should be replaced by constant symbols or closed terms with specific meaning in M. However, if some meaning is defined or understood for these variables, and we are arguing in an informal sense rather than a picky and pedantic way, we can use this understood meaning to make sense of
So Kaye doesn’t spell out the usual Tarksian semantics built on its picky and pedantic account of how to handle open wffs. Then Ch. 10 gives us a Henkin-style proof via Zorn’s Lemma that if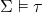 
, where 
is a set of sentences and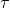 
is a sentence, then 
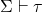(so those familiar with more standard presentation will want to work out just how Kaye can do this while not having spelt out a Tarskian semantics).
Ch. 11, after introducing the notion of countability, shows that in a countable language a consistent set of sentences will have a countable model. It then proves an upward L-S theorem, and takes a first look at ideas like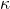 
-categoricity, mentioning Morley’s theorem. Finally, Ch. 12 briefly but clearly discusses non-standard analysis.
Overall, this core of Kaye’s book could certainly make for interesting supplementary reading for someone starting out on FOL, casting light on some key ideas from somewhat unusual directions. But I don’t think it is mere conservatism that would make me reluctant to recommend anyone starting here.
The starred sections which end every chapter are of varying levels of difficulty/sophistication, but almost all are interesting. In particular, Ch. 2 adds a section saying more about Choice and Zorn’s Lemma, making this chapter a useful resource. Ch. 7 adds a little about complexity, P and NP, just enough to whet the reader’s appetite for more. Ch. 10 has two additional sections, one on compactness in logic and topology, and another (quite substantial) on omitting types. The last section of Ch. 12 continues the story about non-standard analysis in an illuminating way. (Some readers dipping into the book might like to start with the starred sections which catch their eye, and backtrack as necessary into the relevant preceding chapters.)
The post Book note: Kaye, The Mathematics of Logic appeared first on Logic Matters.
