Book note: Marker, An Invitation to Math. Logic, I & II

David Marker, the author of what has become a modern classic on model theory, has recently published  An Invitation to Mathematical Logic (Springer, 2024). “My goal was to write a text for a one-semester graduate-level introduction to mathematical logic, one that I would have liked to learn from when I was a student, and one I would like to teach from as a professor.” Part I of the book, ‘Truth and Proof’ is on first-order logic and theories and the structures for interpreting them. Part II is on ‘Elements on Model Theory’. I’ll say something about these first two Parts here, and I’ll discuss Part III ‘Computability’ and Part IV ‘Arithmetic and Incompleteness’ in a follow-up post. (The book doesn’t discuss set theory.)

Compare these two presentations of a familiar result. Here’s Exhibit A:

And here is Exhibit B:

Which do you prefer? I vote for Exhibit A. The couple of sentences of the preamble, “The key idea is …”, are just what is needed to fix our understanding of the Tarski–Vaught claim. And then the balance of the ensuing proof is that bit nicer. The trivial cases for the induction are relegated to exercises, and the structure of the remaining case slightly better signalled (“Conversely”). [Imagine the bookwork part of an exam done under time pressure: you’d prefer something along the lines of Exhibit A, wouldn’t you, as showing the student had seen what was important?]

Now, Exhibit A is from Kirby’s excellent An Invitation to Model Theory. Exhibit B is from Marker’s new Invitation. Of course I don’t want to make anything hang on this one example. But I do think the difference between Marker and (in this case) Kirby covering this same material is in fact rather typical. I could have chosen other examples and other contrasting authors (I’ve just picked a nice short illustration). And we’d similarly see that, on the one hand, Marker tends to short-change the reader when it comes to those useful orientating sentences or two which can be so helpful (the classroom asides, the “look at it this way” guides). And on the other hand, some of his proofs can be a little ploddingly flat-footed, leaving the reader to distinguish the interesting moves from the bits where we are just joining-up-the-dots. The cumulative effect is to make Parts I and II of Marker’s book that bit less reader-friendly (especially for self-study) than he intends.

In just a little more detail, Part I (64 pp.) has four chapters. Ch. 1, ‘Languages, Structures, and Theories’ provides a terse introduction, rather short on motivations and explanations (a quite trivial but characteristic example: we are flatly told that 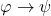is an abbreviation of 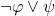, take it or leave it, end of story: so much for calming the common student discomfort — graduate student or otherwise — with the conventional treatment of the conditional!). We get the same briskness in Ch. 2, ‘Embeddings and Substructures’ (where we find Exhibit B). The short Ch. 3 introduces one proof system for FOL, a sequent calculus, in which proofs are simple linear arrays, Hilbert-style. A perfectly serviceable system, but there’s no hint at all about different ways of doing things. Then Ch. 4 proves completeness, in places a bit laboriously. Marker does bring out nicely why the story goes a bit differently for countable languages and uncountable languages (needing Zorn’s Lemma or an equivalent in the second case). But on the other hand — the student reader might reasonably ask — given that all the examples in Ch. involves small finite languages, exactly why might we care about the uncountable case? I don’t think we are told.

These chapters are of course all done perfectly respectably: but just how inviting are they? I, for one, didn’t find them particularly so, and I at least had the advantage of already knowing what was supposed to be going on.

Part II (71 pp.) again has four chapters. Ch. 5 is on compactness (introduced as a simple consequence of completeness), starting with some elementary applications but soon turning to examples you’ll need more mathematical background to understand. Ch. 6 is a somewhat dense introduction to ultraproducts, giving us another proof of compactness. Ch. 7 begins on the basic idea of quantifier elimination; but soon, as with Ch. 8, we are into fairly hardcore algebraic applications — fine for the graduate pure mathematicians with some serious algebra under their belt who are perhaps Marker’s core intended audience, but again not done invitingly enough (say I) to draw in other readers whose prime interests are more logical.

So far, then, I have to confess to being rather disappointed by a book I had higher expectations of. But how does the (perhaps less ambitious) second half of the book go?

The post Book note: Marker, An Invitation to Math. Logic, I & II appeared first on Logic Matters.