Book note: Halbeisen & Krapf, Gödel’s Theorems and Zermelo’s Axioms

A standard menu for a first mathematical logic course might be something like this: (1) A treatment of the syntax and semantics of FOL, presenting a proof system or two, leading up to a proof of a Gödel’s completeness theorem (and then a glance at e.g. the compactness theorem and some initial implications). (2) An introduction to formal arithmetic, a little about computability, with Gödel’s incompleteness theorems a highlight. (3) A modest amount of set theory, looking e.g. at the way number systems including the reals can be constructed in set theory; a first encounter with cardinals, ordinals and Choice; then the formalization of set theory in ZFC. With all this leading to an emerging sense of (4) the limitations of first-order theories and the ubiquity of non-standard models.

So an attractive, accessible, relatively short, book covering Gödel’s Theorems (completeness/incompleteness) and Zermelo’s Axioms (and why we need a bit more than Zermelo’s original proposals) could indeed have a grateful readership.

But Lorenz Halbeisen and Regula Krapf’s promisingly titled book (published by Birkhäuser in 2020) is not that book. It does tick the box of being relatively short (x + 236 pp.). However — to be blunt about it — this is not particularly reader-friendly, often unnecessarily hard going, and there are much better options, particularly for self-study.

Part I introduces FOL, initially in Hilbert-style (with a selection of axioms presented in a take-it-or-leave-it spirit).  Then we get what is advertised as a natural deduction system, though by p. 24 it is beginning to look more like a sequent calculus (in a way that could confuse the reader). On p. 30 we get a trivial syntactic result labelled as the compactness theorem (in a way that could again confuse the reader who was seen standard talk of compactness elsewhere). Then we get a pretty messy introduction to the semantics of FOL.

Part II proves the completeness theorem (for countable signatures), done Henkin-style. Somehow the rather neat elegance that such proofs can have is quite lost in the telling: would the student new to this come away with a good sense of the fundamental ideas? — I doubt it.

Part III starts with a short chapter on standard and non-standard models of PA, before actually looking in the next chapter at how arithmetic can be done in PA. There follows a twenty-page chapter hacking through the arithmetization of syntax for PA: ok, this is necessarily a messy business, but it is certainly done more accessibly and more attractively elsewhere.

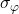Then we get the key chapter on the first incompleteness theorem. Once more, I can’t say that this is done in a reader-friendly way. The diagonalization lemma is plucked out of the sky; and there’s careless talk of the kind we warn our students against — the lemma “allows us to make self-referential statements, i.e. for a formula with one free variable it provides a sentence which states ‘I have the property ’. ” No it doesn’t. And then the initial proof of incompleteness on p. 112 will puzzle readers who’ve seen (or are about to see) other presentations — how do we get that PA doesn’t prove a fixed point of 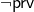without mentioning -consistency?

Moving on, we do get a full-dress eight-page proof of the second incompleteness theorem for PA, and in particular of the third derivability condition, i.e. it’s shown that PA proves 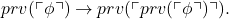It probably sounds ungrateful, but is this really what we want or need in an introductory book? Only if particularly nicely done, which it isn’t.

Part IV is on set theory, starting with a twenty page chapter on the axioms of ZFC, but also  explaining the set-theoretic definitions of functions and relations, saying something about Choice, and introducing ordinals and cardinals. All surely far too fast for the student for whom this really is all new.

The remaining chapters are on models of set theory, standard and non-standard; on ultrafilters and ultra products (and so completeness for FOL with uncountable signatures); briefly again on non-standard models of PA; and then on real numbers, non-standard models of the reals, and a little on non-standard analysis. My sense is that these final chapters — which are worthwhile reading for someone who has got the basics nailed down elsewhere — is where the authors’ real interest lies.

So my summary recommendation: you can cheerfully ignore what’s gone before (there are many better options for introducing their material), but students with enough background might well find the last four chapters, some 50 pages, interesting and profitable.

The post Book note: Halbeisen & Krapf, Gödel’s Theorems and Zermelo’s Axioms appeared first on Logic Matters.