Bernoulli Numbers and the Harmonic Oscillator

I keep wanting to understand Bernoulli numbers more deeply, and people keep telling me stuff that’s fancy when I want to understand things simply. But let me try again.

The Bernoulli numbers can be defined like this:

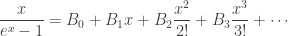
and if you grind them out, you get

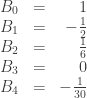
and so on. The pattern is quite strange.

Bernoulli numbers are connected to hundreds of interesting things. For example if you want to figure out a sum like

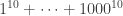
you can use Bernoulli numbers—indeed Jakob Bernoulli boasted

It took me less ...