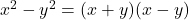Frege on seeing what is in front of his nose, revisited

There’s a new piece just published by Jamie Tappenden with the promising title ‘Following Bobzien: Some Notes on Frege’s Development and Engagement with his Environment’ (History and Philosophy of Logic https://doi.org/10.1080/01445340.2024...). But, for me a bit disappointingly, this turns out to be — yet once more — mostly about Frege’s engagement with, in a broad sense at any rate, philosophers. Yet didn’t the early Frege think of himself as a mathematician? So I’d certainly like to know more about his mathematical environment: for example, what texts on analysis was  Frege initially most directly acquainted with and how did these feed into and shape his work in Begriffsschrift?

A few years ago, I posted here a note relevant to this, and here it is again, slightly tidied up.

Take a mathematician of Frege’s generation, accustomed to writing the likes of

(1)

(2) If , then or ,

and much fancier things, of course!

Whatever confused thoughts about ‘variables’ people may or may not have had once upon a time, they had surely been more or less dispelled before the 1870s, if not by Balzano’s 1817 Rein analytischer Beweis (though probably that was not widely enough read?), at least by Cauchy’s great 1821 Cours d’analyse which everyone serious will have read.

Both Bolzano and Cauchy will take a claim like (1) to be true just when the equation holds for each value that x can take (each real number, as it might be, or each integer, say) — i.e. they clearly gloss such claims written with variables as claims holding for any value of x. Likewise, (2) will be glossed as saying that there are just two values of x, namely the stated ones, where the equation holds. The mathematicians of the day, at least when on their best behaviour, could be pretty decently clear about this. (Yes, reading Cauchy’s Cours, we will be very struck that after only a few pages we encounter “infinitely small quantities”: indeed the very first numbered theorem is about such quantities. So we are definitely in a pre-Weierstrassian world! But on the other hand, I don’t think we encounter anything that we should find too uncomfortable about variables and their values.)

But then it seems to be only the tiniest of steps to say outright that an ideal notation for such claims as (1) might explicitly have the form ‘for any value of 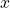, 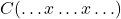’, and that such an explicit formulation is true when ‘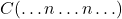’ is true whatever ‘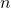’ might name. So — looked at from this angle — the wonder is not that Frege came up with his basic account of the logical form of expressions of mathematical generality like (1) but that no one had quite said as much before.

If you go back to Bolzano’s 1810 Beyträge, what happens there (with hindsight) seems very odd indeed. After all, here is someone who within a few years — in his 1816 Der binomische Lehrsatz and (even more) the 1817 Rein analytischer Beweis — is very clear indeed about variables and their use, when making essential practical use of quantification in talking about continuity etc. Yet in the earlier Beyträge, his Contributions to a Better-Grounded Presentation of Mathematics, when Bolzano turns to talking about logic and the principles of deduction, he looks quite antediluvian — and as far as I know he never revisited the logical basics in order to try to do better. OK, he says the mathematician will need more principles than we’ll find in the traditional syllogistic, and your hopes rise just for a moment: but the additional principles he comes up with are such a very limited and disappointing lot — the likes of A is an M, A is an N, so A is an M-and-N. It seems that the Bolzano of the Beyträge is — despite his disagreements and amendments — so thoroughly soaked in Kant and in broadly Aristotlean logic that he just can’t see what is right in front of his nose in the mathematician’s use of variables.

At least here, then, Frege’s originality — it might be said — is not depth of insight but his unabashed willingness to take the mathematician’s usage of the likes of (1) and (2) at bald face value, and to not try to shoehorn such generalizations into the canonical forms sanctioned by received logical wisdom. It is as if his now standard treatment of generality is a very happy result of Frege’s actually starting off knowing little of previous logic and philosophy.

I have often wondered, then, if Frege’s philosophical commentators have tended to see his basic discovery of a quantifier(-for-scoping)/variable notation as a more stunning discovery than it was. Take the pre-Frege usage of mathematician’s variables-of-generality at face value, without preconceptions (“don’t think, look” as Wittgenstein might say). Then note that we must e.g. distinguish generalizing a negation () and negating a generalization (it’s not true in general that ) — so if we are going to use a symbol for negation we are going to somehow have to mark relative scopes. And — implementation details apart — we are already more or less there!

Moreover, in Begriffsschrift and pieces written around that time, Frege’s concern seems explicitly to be very much with regimenting mathematical language (i.e. formalizing the logical bits of it to go along with the already common formal expressions we use for the non-logical bits, showing how adding the logical bits allows us to neatly cut down on the non-logical primitives by giving us the resources to define more complex concepts out of simpler ones, etc. etc.). He says remarkably little — except in using a few toy examples like the ‘Cato killed Cato’ one — about ordinary, non-mathematical, language more generally. So e.g. Dummett’s reading of Frege from the very beginning as aiming for a story about the real underlying logical structure of ordinary language generalizations is arguably considerable over-interpretation: Frege seems at least in Begriffsschrift to be much more in the business of giving us a somewhat tidied up replacement for informal ways of talking which is useful in regimenting science — one modelled closely upon, to borrow his phrase, the formula language of arithmetic.

Saying all this is of course not for a moment to underplay the depth of Frege’s reflections consequent on his discovery of the quantifier/variable notation! But let’s start slowly: I would very much like to know more about the history of maths, in particular on  how variables were regarded in early 19th century mathematics. I’d like to know more about Frege’s mathematical environment, and so understand better the nature of the clarificatory step Frege was taking in regimenting informal mathematical discourse in quantifier/variable style as he does.

The post Frege on seeing what is in front of his nose, revisited appeared first on Logic Matters.