How bewildering is the Yoneda embedding?

There’s now another one-chapter update for Category Theory II.

There’s some minor earlier tinkering, but Chapter 37 has been considerably revised. The proofs leading up to what I call the Restricted Yoneda lemma and the Yoneda Embedding Theorem have been tidied up, and should be much clearer. And the final section “Yoneda meets Cayley” — which was a mess, almost incoherently so — is now crisp and clear. I hope!

Tom Leinster has written “The level of abstraction in the Yoneda Lemma means that many people find it quite bewildering.” While Awodey calls it “the single most used result” of category theory. So: bewildering but centrally important?

Well, I really do hope the decaffeinated version of Yoneda in Chapter 37 really is plain sailing. There’s basically one small idea — you can use a 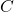-arrow 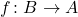very simply to construct a natural transformation between hom-functors 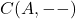and 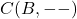— and then all the rest is pretty much applying definitions in obvious ways. So far, I hope, not bewildering at all!

The post How bewildering is the Yoneda embedding? appeared first on Logic Matters.