Horror's Greatest Hits

A Curious Integral

On Mathstodon, Robin Houston pointed out a video where Oded Margalit claimed that it’s an open problem why this integral:

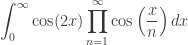
\displaystyle{ \int_0^\infty\cos(2x)\prod_{n=1}^\infty\cos\left(\frac{x}{n} \right) d x }

is so absurdly close to 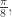\frac{\pi}{8}, but not quite equal.

They agree to 41 decimal places, but they’re not the same!

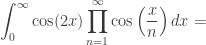
\displaystyle{ \int_0^\infty\cos(2x)\prod_{n=1}^\infty\cos\left(\frac{x}{n}\right) d x } =
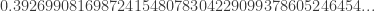
0.3926990816987241548078304229099378605246454...

while

\frac\pi 8 =
0.3926990816987241548078304229099378605246461...

So, a bunch of us tried to figure out what was going on.

Jaded nonmathematicians told us it’s just a coincidence, so what is there to explain? But of course an agreement this close is unlikely to be “just a coincidence”. It might be, but you’ll never get anywh...

View more on John C. Baez's website »
 •  0 comments  •  flag
Share on Twitter
Published on January 04, 2023 14:04
No comments have been added yet.


John C. Baez's Blog

John C. Baez
John C. Baez isn't a Goodreads Author (yet), but they do have a blog, so here are some recent posts imported from their feed.
Follow John C. Baez's blog with rss.