Avigad, MLC — 1: What are formulas?
I noted before that Jeremy Avigad’s new book Mathematical Logic and Computation has already been published by CUP on the Cambridge Core system, and the hardback is due any day now. The headline news is that this looks to me the most interesting and worthwhile advanced-student-orientated book that has been published recently.
I’m inspired, then, to blog about some of the discussions in the book that interest me for one reason or another, either because I might be inclined to do things differently, or because they are on topics that I’m not very familiar with, or (who knows?) maybe for some other reason. I’m not planning a judicious systematic review, then: these will be scattered comments shaped by the contingencies of my own interests!
Chapter 0 of MLC is on “Fundamentals”, aiming to “develop a foundation for reasoning about syntax”. So we get the usual kinds of definitions of inductively defined sets, structural recursion, definitions of trees, etc. and applications of the abstract machinery to defining the terms and formulas of FOL languages, proving unique parsing, etc.
This is done in a quite hard-core way (particularly on trees), and I think you’d ideally need to have already done a mid-level logic course to really get the point of various definitions and constructions. But A [Avigad, the Author, of course!] notes that he is here underwriting patterns of reasoning that are intuitively clear enough, so the reader can at this point skim, returning later to nail down various details on a need-to-know basis.
But there is one stand-out decision that is worth pausing over. Take the two expressions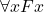 
and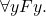 
The choice of bound variable is of course arbitrary. It seems we have two choices here:
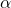-equivalent, as they say) are always interderivable, are logically equivalent too.Say that formulas proper are what we get by quotienting expressions by 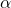-equivalence, and lift our first-shot definitions of e.g. wellformedness for expressions of FOL to become definitions of wellformedness for the more abstract formulas proper of FOL.Now, as A says, there is in the end not much difference between these two options; but he plumps for the second option, and for a reason. The thought is this. If we work at expression level, we will need a story about allowable substitutions of terms for variables that blocks unwanted variable-capture. And A suggests there are three ways of doing this, none of which is entirely free from trouble.
Distinguish free from bound occurrences of variables, define what it is for a term to be free for a variable, and only allow a term to be substituted when it is free to be substituted. Trouble: “involves inserting qualifications everywhere and checking that they are maintained.”Modify the definition of substitution so that bound variables first get renamed as needed — so that the result of substituting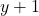
for 
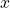in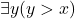 
is something like 
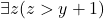. Trouble: “Even though we can fix a recipe for executing the renaming, the choice is somewhat arbitrary. Moreover, because of the renamings, statements we make about substitutions will generally hold only up to 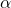-equivalence, cluttering up our statements.”Maintain separate stocks of free and bound variables, so that the problem never arises. Trouble: “Requires us to rename a variable whenever we wish to apply a binder.”I’m not quite sure how we weigh the complications of the first two options against the complications involved in going abstract and defining formulas proper by quotienting expressions by 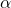– equivalence. But be that as it may. The supposed trouble counting against the third option is, by my lights, no trouble at all. In fact A is arguably quite misdescribing what is going on in that case.
Taking the Gentzen line, we distinguish constants with their fixed interpretations, parameters or temporary names whose interpretation can vary, and bound variables which are undetachable parts of a quantifier-former we might represent ‘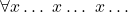
’. And when we quantify 
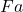to get 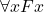we are not “renaming a variable” (a trivial synactic change) but replacing the parameter which has one semantic role with an expression which is part of a composite expression with a quite different semantic role. There’s a good Fregean principle, use different bits of syntax to mark different semantic roles: and that’s what is happening here when we replace the ‘
’ by the ‘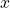’, and at the same time bind with the quantifier 
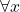(all in one go, so to speak).
So its seems to me that option 1c is markedly more attractive than A has it (it handles issues about substitution nicely, and meshes with the elegant story about semantics which has 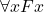true on an interpretation when 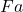is true however we extend that interpretation to give a referent to the temporary name ). The simplicity of 1c compared with option 2 in fact has the deciding vote for me.
The post Avigad, MLC — 1: What are formulas? appeared first on Logic Matters.
