NF is consistent
Randall Holmes has been claiming a proof for about a decade, and recently posted yet another improved update of his proof on arXiv.
A while back, there was some very interesting discussion about the possibility of formalising the proof using a proof assistant like Lean. There’s now some relevant local news, which I get from Thomas Forster.
Roughly speaking, the proof has three components. (1) Randall proved over twenty-five years ago that NF is consistent if what he called Tangled Type Theory, TTT, is. Arm waving, the latter is what you from the simple theory of types if you allow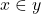 
to be well-formed even when 
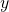is more than one type higher 
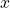(in other words, we relax the usual requirement that 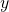here is exactly one type higher than 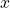), so there is an 
relation between any lower level and any higher level. This relative consistency claim is unproblematic.
(2) TTT is a seemingly rather wild theory. But Holmes now aims to present a Frankel-Mostowski-style construction that purports to be a model of TTT. The devil is in the contorted(?) detail: do we get a coherent description of a determinate structure?
(3) Assuming that stage (2) is successful in at least describing a kosher structure that a ZF-iste can happily accept as such, there then is the task of verifying that it really is a model of TTT.
Now, over the last few weeks, a bunch of maths students here have been working on a summer project arranged by Thomas (with a lot of Zoomed input from Randall) to formally verify the consistency proof in Lean, by first checking (2) that the model is coherently constructed, and then going on to check (3) it really is a model of TTT. And I understand the state of play to be this: that first of these stages is successfully more or less completed. And it has in the process become intuitively clear — said Thomas — that the defined structure is indeed a model of TTT. Dotting the i’s and crossing the t’s and implementing a Lean check that the model satisfies a certain finite axiomatization of TTT will take more time than there is left in this summer’s project (the students have lives to lead!). But with (2) secure, it looks as if Holmes indeed has his claimed proof, though its final best-form shape remains to be settled.
If that’s right, Holmes has settled one of the oldest open problems in set theory. Though quite what the wider significance of this, I’m frankly not so sure. Will a consistency proof (of a decidedly tricksy-seeming kind) really make us look much more kindly on NF? Should it?
The post NF is consistent appeared first on Logic Matters.
