Distribution of tossed coins, a reminder

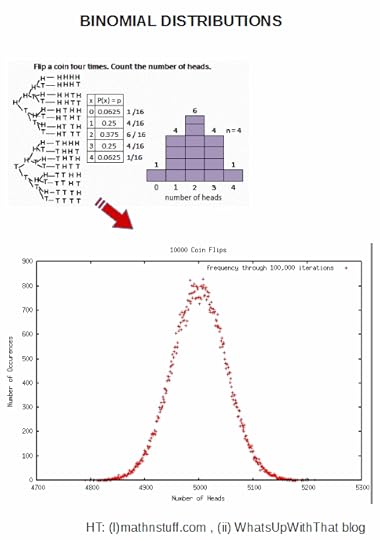
We see the binomial distribution of coin-flipping possibilities, here based on 10,000 actual tosses iterated 100,000 times, also indicating just how tight the peak is, mostly being between 4,850 and 5,150 H:

Thus we see the roots of discussions on fluctuations:

Note, not coincidentally, sqrt (10^4) = 10^2, or 100.

(Compare the bulk of the 10,000 coin toss plot on 100 k repetitions, centred on 5000h, with +/- 100 capturing the main part. Obviously possibilities run from 0 H to 10,000 H but there is a sharply peaked clustering about the “average”.) END

Copyright © 2022 Uncommon Descent . This Feed is for personal non-commercial use only. If you are not reading this material in your news aggregator, the site you are looking at is guilty of copyright infringement UNLESS EXPLICIT PERMISSION OTHERWISE HAS BEEN GIVEN. Please contact legal@uncommondescent.com so we can take legal action immediately.
Plugin by Taragana