On apparently not avoiding explosion after all

In hidden place, so lett my days fort... Logic job at Warwick

On apparently not avoiding explosion after all

table.center { width: 20%; margin-left: auto; margin-right: auto; text-align: center;}table.center2 { width: 40%; margin-left: auto; margin-right: auto; text-align: center;}

I’ve been drafting some notes on “Other logics” for Beginning Mathematical Logic, and am currently writing something about relevant logics. A seemingly obvious point occurred to me about a familiar semantic story for First Degree Entailment — one that has surely been made before, but (because I haven’t read enough, or because my eyes glazed over at some crucial point, or because my memory is playing up) I can’t recall seeing discussed. So I’m wondering what the fan of that sort of semantic story says in response. Here’s an excerpt from what I’ve drafted (which also includes stuff about disjunctive syllogism as that is relevant in the context from which this comes), raising the point in question:

Logicians are an ingenious bunch. And it isn’t difficult to cook-up a formal system for a propositional language equipped with connectives written “ $\neg$ ” and “ $\lor$ ’ for which analogues of disjunctive syllogism and explosion don’t generally hold.

For example, suppose we build a model which assigns every wff one of four values. Label the values T, B, N, F. And suppose that, given an assignment of such values to atomic wffs, we compute the values of complex wffs using the following tables:

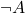$\neg A$ TFBBNNFT $A \lor B$ TBNFTTTTTBTBTBNTTNNNTBNF

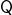These tables are to be read in the obvious way. So, for example, if $\mathsf{P}$ takes the value B, and $\mathsf{Q}$ takes the value N, then [image error] takes the value B and 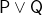$\mathsf{P \lor Q}$ takes the value T.

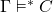Suppose in addition that we define a quasi-entailment relation as follows: some premisses [image error] entail a given conclusion [image error] — in symbols $\Gamma \vDash^* C$ — just if, on any valuation which makes each premiss either T or B, the conclusion is also either T or B.

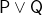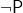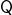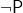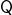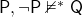Then, lo and behold, the analogue of disjunctive syllogism is not always a correct entailment: on the same suggested valuations, both $\mathsf{P \lor Q}$ and $\neg\mathsf{P}$ are either T or B, while $\mathsf{Q}$ is N, so [image error]. And we don’t always get explosion either, since both $\mathsf{P}$ and $\neg\mathsf{P}$ are B while $\mathsf{Q}$ is N, so $\mathsf{P, \neg P \nvDash^* Q}$ .

Which is all fine and good: but what is the logical significance of this construction? Can we give some semantic interpretation to the assignments of values, so that our tables really do have something to do with negation and disjunction, and so that entailment does become a genuine consequence relation?

Well, suppose — just suppose! — that propositions can not only be plain true or plain false but can also be both true and false at the same time, or neither true nor false. In a phrase, suppose there can be truth-value gluts and truth-value gaps.

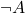Then there will indeed be four truth-related values a proposition can take — T (true), B (both true and false), N (neither), F (false). And, interpreting the values like that, the tables we have given arguably respect the meaning of `not’ and `or’. For example, if is both true and false, the same should go for $\neg A$ . While if is both true and false, and 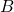is neither, then $A \lor B$ is true because its first disjunct is, but it isn’t also false as that would require both disjuncts to be false (or so we might argue). Moreover, the intuitive idea of entailment as truth-preservation is still reflected in the definition of entailment, which says that if premisses are all true (though maybe false as well), the conclusion is true (though maybe false as well).

But what on earth can we make of that supposition that some propositions are both true and false at the same time? This will seem simply absurd to most of us.

However, a vocal minority of philosophers do famously argue that while, to be sure, regular sentences
can’t be both true or false, the likes of the paradoxical liar sentence “This sentence is false” can be. It is fair to say that few are persuaded by this line. However, I don’t want to get entangled in that debate here. For it isn’t clear that this extravagant idea actually helps very much. Suppose we do countenance the possibility that some special sentences have the deviant status of being both true and false (or being neither). Then we might reasonably propose to add to our formal logical apparatus an operator ‘!’ to signal that a sentence is not deviant in that way, governed by the following table:

TTBFNFFT

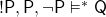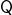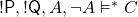Why not? After all, we have use for such a sign, given that we are confident of many sentences in use that they are not deviant cases. But then note that $\mathsf{!P, P, \neg P \vDash^* Q}$ . And similarly, if say $\mathsf{P}$ and $\mathsf{Q}$ are the atoms present in , then $\mathsf{!P, !Q}, A, \neg A \vDash^* C$ always holds. Yet this modified form of explosion — when built out of regular claims, a contradictory pair entails anything — is surely just as unwelcome as the original unrestricted form of explosion. (Parallel remarks apply to disjunctive syllogism. We still have, e.g., $\mathsf{!P, \neg P, P \lor Q \vDash^* Q}$ .)