The Kuramoto–Sivashinsky Equation (Part 5)

In Parts 3 and 4, I showed some work of Cheyne Weis on the ‘derivative form’ of the Kuramoto–Sivashinksy equation, namely

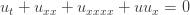
Steve Huntsman’s picture of a solution above gives you a good feel for how this works.

Now let’s turn to the ‘integral form’, namely

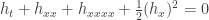
This has rather different behavior, though it’s closely related, since if 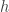is any solution of the integral form then

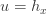
is a solution of the derivative form.

Cheyne drew a solution of the integral form:

You’ll immediately see the most promi...