Information Geometry (Part 19)

Last time I figured out the analogue of momentum in probability theory, but I didn’t say what it’s called. Now I will tell you—thanks to some help from Abel Jansma and Toby Bartels.

SURPRISE: it’s called SURPRISAL!

This is a well-known concept in information theory. It’s also called ‘information content‘.

Let’s see why. First, let’s remember the setup. We have a manifold

whose points 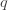are nowhere vanishing probability distributions on the set We have a function

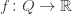
called the Shannon entro...