The Koide Formula

There are three charged leptons: the electron, the muon and the tau. Let 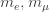and 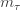be their masses. Then the Koide formula says

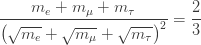
There’s no known reason for this formula to be true! But if you plug in the experimentally measured values of the electron, muon and tau masses, it’s accurate within the current experimental error bars:

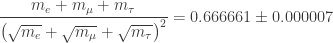
Is this significant or just a coincidence? Will it fall apart when we measure the masses more accurately? Nobody knows.

Here’s something fun, though:

Puzzle. Sho...