Decimal Digits of 1/π²

This formula may let you compute a decimal digit of 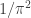$1/\pi^2$ without computing all the previous digits:

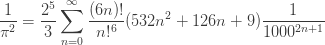
$\displaystyle{ \frac{1}{\pi^2} = \frac{2^5}{3} \sum_{n=0}^\infty \frac{(6n)!}{n!^6} (532n^2 + 126n + 9) \frac{1}{1000^{2n+1}} }$

It was discovered here:

• Gert Almkvist and Jesús Guillera, Ramanujan-like series for 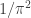$1/\pi^2$ and string theory, Experimental Mathematics, 21 (2012), 223–234.

They give some sort of argument for it, but apparently not a rigorous proof. Experts seem to believe it:

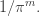
It’s reminiscent of the famous Bailey–Borwein–Plouffe formula for $\pi:$

$\displaystyle{ \pi = \sum_{n = 0}^\infty \frac{1}{16^n} \left( \frac{4}{8n + 1} - \frac{2}{8n + 4} - \frac{1}{8n + 5} - \frac{1}{8n + 6} \right) }$

This lets yo...

Like • 0 comments • flag

Published on October 10, 2020 09:23

No comments have been added yet.

John C. Baez's Blog

John C. Baez isn't a Goodreads Author (yet), but they do have a blog, so here are some recent posts imported from their feed.