Gödel Without Tears, slowly, 9

Today’s chapter is about ‘Expressing and capturing the primitive recursive functions’. We prove (in reasonable detail) that although the language of basic arithmetic 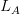only has the successor, addition and multiplication functions built in, we can in fact form a 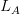wff to express any primitive recursive function we pick. And then we prove (or rather, wave our arms at a proof) that even the weak Robinson Arithmetic can reprsent or ‘capture’ every primitive recursive function.

Even cutting lots of corners, this chapter is inevitably a bit fiddly. But one nice idea we meet is the use of a coding device for handling finite sequences of numbers. I try to make clear (a) how having such a device will enable us to express/capture primitive recursive functions, while (b) distinguishing the neat general coding idea from Gödel’s particular implementation of the device using his beta function.

The post Gödel Without Tears, slowly, 9 appeared first on Logic Matters.