Diễn đạt

Hai câu dưới đây copy từ wiki, nội dung lãng mạn:

Câu 1: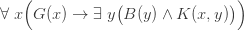

Câu này đọc là: Với từng cô gái (trong tất cả các cô gái) sẽ tương ứng (có) vài chàng trai (là bất cứ ai trong các chàng trai) là người mà cô gái đã hôn.

Câu 2: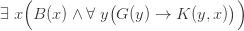

Câu này đọc là: Có vài chàng trai (cụ thể) nào đó mà tất cả các cô gái đã hôn.

*

Còn hai câu phát biểu dưới đây, tôi chép lại của ông Penrose, là hai cách phát biểu khác nhau của Định lý Fermat.

Câu 3: ~

Câu 4:

Hai câu này nếu đọc thành tiếng người, ở đây là tiếng Việt, sẽ là:

Câu 3: Không tồn tại các số tự nhiên w,x,y,z sao cho x cộng một lũy thừa lên w cộng ba rồi cộng với y cộng một lũy thừa lên w cộng ba bằng với z cộng một lũy thừa w cộng ba.

Câu 4: Với mọi số tự nhiên w,x,y,z không tồn tại các số sao cho x cộng một lũy thừa lên w cộng ba rồi cộng với y cộng một lũy thừa lên w cộng ba bằng với z cộng một lũy thừa w cộng ba.

*

Còn câu này:

Câu 5: 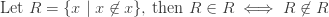chính là Nghịch lý Russel.

Phiên bản giản dị của nó như sau: Giả sử có một anh thợ cắt tóc, anh này cắt tóc cho tất cả những người đàn ông không tự cắt tóc cho mình, và chỉ cắt tóc những người đàn ông không tự cắt cho mình. Khi ta hỏi, anh thợ cắt tóc này có nên tự cắt cho chính mình hay không, thì nghịch lý bắt đầu lộ diện.

Có thể anh đạo diễn phim Parasite, anh Bong Joon-ho, có học về logic, nên các tình tiết trong phim của anh như “Mother”, “Memories of Murder” cứ gài người xem buộc phải “động não”. Và rồi các “nghịch lý” từ từ xuất hiện, tạo ra sức hấp dẫn của bộ phim, cho đến tận phút cuối cùng.