Two-place functions aren't one-place functions, are they?
Here's a small niggle, that's arisen rewriting a very early chapter of my Gödel book, and also in reading a couple of terrific blog posts by Tim Gowers (here and here).
We can explicitly indicate that we are dealing with e.g. a one-place total function from natural numbers to natural numbers by using the standard notation for giving domain and codomain thus:  . What about two-place total functions from numbers to numbers, like addition or multiplication?
. What about two-place total functions from numbers to numbers, like addition or multiplication?
"Easy-peasy, we indicate them thus:  ."
."
But hold on! 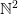 is standard shorthand for
is standard shorthand for 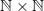 , the cartesian product of
, the cartesian product of 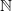 with itself, i.e. the set of ordered pairs of numbers: and an ordered pair is standardly regarded as one thing with two members, not two things. So a function from
with itself, i.e. the set of ordered pairs of numbers: and an ordered pair is standardly regarded as one thing with two members, not two things. So a function from 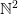 to
to 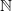 is in fact a one-place function that maps one argument, an ordered pair object, to a value, not (as we wanted) a two-place function mapping two arguments to a value.
is in fact a one-place function that maps one argument, an ordered pair object, to a value, not (as we wanted) a two-place function mapping two arguments to a value.
"Ah, don't be so pernickety! Given two objects, we can find a pair-object that codes for them, and we can without loss trade in a function from two objects to a value to a related function from the corresponding pair-object to the same value."
Yes, sure, we can eventually do that. And standard notational choices can make the trade invisible. For suppose we use 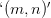 as our notation for the ordered pair of
as our notation for the ordered pair of 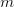 with
with 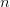 , then
, then 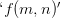 can be parsed either way, as representing a two-place function with arguments
can be parsed either way, as representing a two-place function with arguments 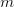 and
and 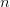 or as a corresponding one-place function with the single argument
or as a corresponding one-place function with the single argument 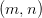 . But the fact that trade between the two-place and the one-place function is glossed over doesn't mean that it isn't being made. And the fact that the trade can be made (even staying within arithmetic, using a pairing function) is a result and not quite a triviality. So if we are doing things from scratch — including proving that there is a pairing function that matches two things with one thing in such a way that we can then extract the two objects we started with — then we do need to talk about two-place functions, no? For example, in arithmetic, we show how to construct a pairing function from the ordinary school-room two-place addition and multiplication functions, not some surrogate one-place functions!
. But the fact that trade between the two-place and the one-place function is glossed over doesn't mean that it isn't being made. And the fact that the trade can be made (even staying within arithmetic, using a pairing function) is a result and not quite a triviality. So if we are doing things from scratch — including proving that there is a pairing function that matches two things with one thing in such a way that we can then extract the two objects we started with — then we do need to talk about two-place functions, no? For example, in arithmetic, we show how to construct a pairing function from the ordinary school-room two-place addition and multiplication functions, not some surrogate one-place functions!
So what should be our canonical way of indicating the domains (plural) and codomain of e.g. a two-place numerical function? An obvious candidate notation is 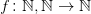 . But I haven't found this used, nor anything else.
. But I haven't found this used, nor anything else.
Assuming it's not the case that I (and one or two mathmos I've asked) have just missed a widespread usage, this raises the question: why is there this notational gap?



