If you take the entries Pascal’s triangle mod 2 and draw black for 1 and white for 0, you get a pleasing pattern:
[image error]
The 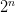 th row consists of all 1’s. If you look at the triangle consisting of the first
th row consists of all 1’s. If you look at the triangle consisting of the first 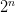 rows, and take the limit as
rows, and take the limit as 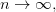 you get a fractal called the Sierpinski gasket. This can also be formed by repeatedly cutting triangular holes out of an equilateral triangle:
you get a fractal called the Sierpinski gasket. This can also be formed by repeatedly cutting triangular holes out of an equilateral triangle:
[image error]
Something nice happens if you interpret the rows of Pascal’s triangle mod 2 as numbers written in binary:
1 = 1
11 = 3
101...
Published on February 05, 2019 09:53
