Every perceptual experience is possibly delusory

(A) Take the following familiar kind of philosophical claim:

Every perceptual experience is possibly delusory!

How do you read this? Do you parse it as

(Every perceptual experience is such that)(it is possible that) it is delusory

or as

(It is possible that)(every perceptual experience is such that) it is delusory?

Do you think that one reading is correct (or at least the strongly preferred reading), and the other incorrect (or at least to be deprecated)? Or do you take (1) to be ambiguous between the ∀♢ reading (2) and the ♢∀ reading (3)?

Peter Geach in Reference and Generality takes it that (1) is unambiguously to be read as (3), with ‘every’ taking narrow scope. Or to be more accurate he talks — at p. 104 of the third edition —  about the fallacy in ‘the transition from “Any sense perception may be illusory” to “Every sense perception may be illusory”.’ I take it that the slight difference in wording is neither here nor there for the current point, and that the fallacy Geach is after is the fallacy of moving from ∀♢ to ♢∀. So indeed Geach is construing his  ‘every’ proposition as ♢∀ (and he doesn’t discern ambiguity).

Interestingly, however, when I asked [on Twitter] about (1), a couple of more-than-respectable voices in different necks of the logical woods agreed with Geach that (1) is not ambiguous — however, they claimed contra Geach that (1) is to be read as (2), i.e. ♢∀. Thus  “I don’t read [this] as ambiguous; [it] seems clearly to have the ∀♢ reading”. And “I can imagine situations where someone uses (1) to be ♢∀, but they’re all situations where someone is using [1] improperly or imprecisely”.

(B) Why is Geach so confident that in his ‘every’ proposition,  like in our (1), the quantifier has narrow scope, while in the corresponding ‘any’ proposition it has wide scope? For him, I think, this view goes with a more general view that ‘every’ takes narrow scope when ‘any’ takes wide scope. Thus contrast

If everyone loves Nerys, then Owen does,
If anyone loves Nerys, then Owen does.

Then, reasonably uncontroversially (and assuming no special emphasis on ‘anyone’), the normal readings of these propositions are different, and these will be regimented respectively as

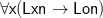
with ‘every’ having narrow scope with respect to the conditional, and vice versa for ‘any’. Indeed, I can imagine Geach armed with his scope principle saying “I can imagine situations where someone uses (1) to be ∀♢, but they’re all situations where someone is using (1) improperly or imprecisely”!!

(C) I take the disagreement between Geach and my twitter correspondents to be a bit of evidence in favour of my own view that both sides are wrong, and that — in the no-doubt corrupted state of modern chat! — (1) is pretty much ambiguous as it stands between the readings (2) and (3).

Now, actually, I don’t want or need to hang anything on this claim in the bit of my intro logic book which I’m re-writing. For when it comes to such quantified claims, it will be agreed on all sides that you do have to take note of questions of scope, even if you disagree about the verdicts. And that’s the crucial point you want when explaining that quantifiers, unlike proper names, have scopes.

Still, I’d be interested to know what other people’s linguistic intuitions are here!  Are you in the No Real Ambiguity camp about (1), and if so do you jump with Geach to the ∀♢ reading, or with some others to the ♢∀ reading? Are you in the You Can Read It Either Way camp? Do you have some other example of an ordinary language proposition mixing a quantifier and a modality which is, you think, a more compelling example of ambiguity? Do tell!

The post Every perceptual experience is possibly delusory appeared first on Logic Matters.