Comment of the Day: But, alas, I think Robert Waldmann ha...

Comment of the Day: But, alas, I think Robert Waldmann has the completely wrong. Draw the graph, Robert! What areas on what graphs does Greg's calculation correspond to? Please tell me!: Robert Waldmann: DeLong & Krugman vs Mankiw and Mulligan III: "Just click the links...

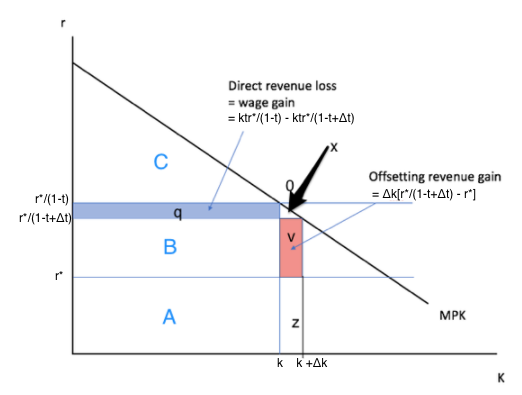
...I finally understand that Brad too is asking a very similarly odd question. The only difference is that Brad considers a tax on capital (tau)k not on capital income (t)f'(k)k. This makes the difference...

No, I do not think that it does.

What does Mankiw think the pretax rate of profit is in the short run after you cut the tax rate from t0 by ��t? The pretax rate of profit was initially:

$ \frac{r}{(1-t_{0})} $

and total pretax income from capital was initally:

$ \frac{k_{0}r}{(1-t_{0})} $

and total government revenue was initially:

$ T_{0} = \frac{t_{0}k_{0}r}{(1-t_{0})} $

As I see it, Mankiw maintains, when calculating the tax revenue loss, that, after the tax cut, the pretax rate of profit is still:

$ \frac{r}{(1-t_{0})} $

So that the amount of revenue collected is:

$ T - ��T = \frac{(t_{0}-��t)k_{0}r}{(1-t_{0})} $

and the change in revenue is:

$ ��T = \frac{��t(k_{0})r}{(1-t_{0})} $

But, as I see it, Mankiw also maintains, when calculating the wage gain, that, after the tax cut, the pretax rate of profit is:

$ \frac{r}{(1-t_{0}+��t)} $

so that there is an extra cash flow ��C per unit of capital arising from the reduced pretax cost of renting capital equal to:

$ ��C = \frac{r}{(1-t_{0})} - \frac{r}{(1-t_{0}+��t)} $

$ ��C = \frac{1-t_{0}+��t - 1+t_{0}}{(1-t_{0})(1-t_{0}+��t)} $

$ ��C = \frac{��t}{(1-t_{0})(1-t_{0}+��t)} $

The total extra cash flow available to pay higher wage is then that times the initial capital stock:

$ ��w = \frac{k_{0}��t}{(1-t_{0})(1-t_{0}+��t)} $

��w is not equal to ��T: there is the extra factor in ��w of:

$ \frac{1}{1-t_{0} (+��t)} $

But this factor does not arise because of the difference between a tax on capital and capital income. It, rather, arises because Mankiw has calculated:

the tax loss assuming that the pretax rate of profit is not immediately impacted by the tax cut,

the cash flow available to pay wages assuming that the pretax rate of profit is immediately impacted by the tax cut.

What if he assumed in making both calculations that the pretax rate of profit did not fall? Then the calculation of the tax revenue loss would be correct. But with no decline in the pretax rate of profit, there is no extra cash flow to pay wages, and so the ratio of wage gain to tax revenue loss is zero.

What if he assumed in making both calculations that the pretax rate of profit did fall to:

$ \frac{r}{(1-t_{0}+��t)} $

?

Then the calculation of the wage gain is correct, but your calculation of the tax revenue loss is in error. Tax revenue falls both because the government is levying a lower rate on pretax profits, and because pretax profits are now lower.

In the long run, as k expands to k(0)+��k, the ratio is greater than one of course���but production function parameters do not drop out...