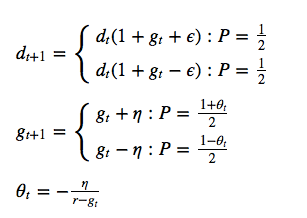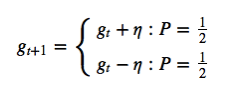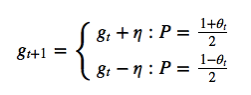Note to Self: Getting in Touch with My Inner Austrian: Toy Stochastic Processes Edition

Note to Self: Getting in Touch with My Inner Austrian: Memo to Self: A Start of a Model...: How can you be an Austrian, and yet have big swings in the desired capital stock���and thus bigger swings in the desired rate of investment���without having to have massive shocks to the current level of technology? How can you get a big downward shock to desired investment without committing yourself to massive technological amnesia?

This is how:

You can do it with two shocks to the dividends paid on a unit of capital: a shock $ \epsilon $ to the level of $ d_{t} $ and a shock $ \eta $ to the growth rate $ g_{t} $ of $ d_{t} $, thus:

Why this dividend process? Because if we then have a required expected rate of return r and a value function $ V(d_{t},g_{t}) = d_{t}v(g_{t}) $, then the one-period arbitrage condition:

$ (1+r)d_{t}v(g_{t}) = d_{t} + E_{t}\left(d_{t}{v(g_{t+1})}\right) $

leads us to

$ (1+r)v(g_{t}) = 1 + \left(\frac{1+g_{t}}{2}\right)\left((1+\theta_{t}){v(g_{t} + \eta)} + (1-\theta_{t}){v(g_{t} - \eta)}\right) $

$ (r-g_{t})v(g_{t}) = 1 + \left(\frac{1+g_{t}}{2}\right)\left((1+\theta_{t}){v(g_{t} + \eta)} + (1-\theta_{t}){v(g_{t} - \eta)} - 2v(g_{t})\right) $

Then simply postulate:

$ v(g_{t}) = \frac{1}{r-g_{t}} $

And find:

$ 1 = 1 + \left(\frac{1+g_{t}}{2}\right)\left(\frac{1+\theta_{t}}{r - g_{t} - \eta} + \frac{1-\theta_{t}}{r - g_{t} + \eta} -\frac{2}{r - g_{t}}\right) $

$ 0 = \left(\frac{(1+\theta_{t})(r - g_{t} + \eta)}{(r - g_{t})^2 - (\eta)^2} + \frac{(1-\theta_{t})(r - g_{t} - \eta)}{(r - g_{t})^2 - (\eta)^2} \right) $

$ 0 = \frac{r - g_{t} + \eta + \theta_{t}r - \theta_{t}g_{t} + \theta_{t}\eta + r - g_{t} - \eta - \theta_{t}r + \theta_{t}g_{t} + \theta_{t}\eta}{(r - g_{t})^2 - (\eta)^2} - \frac{2}{r - g_{t}} $

$ 0 = \frac{2(r - g_{t}) + 2\theta_{t}\eta}{(r - g_{t})^2 - (\eta)^2} - \frac{2}{r - g_{t}} $

$ \frac{1}{r - g_{t}} = \frac{(r - g_{t}) + \theta_{t}\eta}{(r - g_{t})^2 - (\eta)^2} $

$ 1 = \frac{(r - g_{t})^2 + \theta_{t}\eta({r - g_{t}})}{(r - g_{t})^2 - (\eta)^2} $

$ - \eta = \theta_{t}({r - g_{t}}) $

$ \theta_{t} = - \frac{\eta}{r - g_{t}} $

Why all the $ \theta_{t} $ terms? Because you cannot have the expected growth rate of dividends $ g_{t} $ random walk. There is some chance it will random walk upwards and valuations will explode, and a chance of valuations exploding in the future means that valuations explode now (if they haven't already exploded). If you just have:

Then if you assume the Gordon equation for your value function, you find that it is wrong, for your arbitrage equation leads to:

$ 1 = 1 + \left(\frac{1+g_{t}}{2}\right)\left(\frac{1}{r - g_{t} - \eta} + \frac{1}{r - g_{t} + \eta} -\frac{2}{r - g_{t}}\right) $

which then generates the unpleasant:

$ 0 = \left(\frac{r - g_{t}}{(r - g_{t})^2 - (\eta)^2} -\frac{1}{r - g_{t}}\right) $

Writing, instead:

with:

$ \theta_{t} = - \frac{\eta}{r - g_{t}} $

imparts just enough downward drift to the random walk of the growth rate $ g_(t) $ to make the Gordon equation the right valuation equation.

You can complain that this process is not stable: with a constantly-applied downward drift to the growth rate, for a large enough valute of $ t $ it is almost surely the case that $ r - g-{t} $ is very large, and thus that valuations are almost surely very low relative to diviedns because dividends will then be almost surely shrinking fast.

So sue me...

(No calculations yet)



Background


Previous posts:

http://www.bradford-delong.com/2017/11/monday-smackdown-trying-to-get-in-touch-with-my-inner-austrian-was-a-bad-mistake-in-2004-and-a-horrible-misjudgement-in-200.html

This ipynb: https://www.dropbox.com/s/3wsggjajbm897zr/2017-11-26%20Getting%20in%20Touch%20with%20My%20Inner%20Austrian.ipynb?dl=0