Begriffsschrift and absolutely unrestricted quantification

We owe to Frege in Begriffsschrift our modern practice of taking unrestricted quantification (in one sense)  as basic. I mean, he taught us how to rephrase restricted quantifications by using unrestricted quantifiers plus connectives in the now familiar way, so that e.g. “Every F is G”  is regimented as  “Everything is such that, if it is F, then it is G” , and some “Some F is G”  is regimented as  “Something is such that it is F and it is G” — with the quantifier prefix in each case now running over everything. And we think the gain in formal simplicity in working with unrestricted quantifiers outweighs the small departure from the logical forms of natural language (and quirks to do with existential import, etc.).

But what counts as the “everything” which our unrestricted quantifiers run over? In informal discourse, we cheerfully let the current domain of quantification be set by context (“I’ve packed everything”,  “Everyone is now here, so we can begin”). And we are adepts at following conversational exchanges where the domain shifts as we go along.

In the context of using a formal first-order language, we require that the domain, i.e. what counts as “everything”, is fixed once and for all, up front: no shifts are then allowed, at least while that language with that interpretation is in force. All changes of what we want to generalize about are to be made by explicitly restricting the complex predicates our quantifiers apply to, as Frege taught us.  The quantifiers themselves stay unrestrictedly about the whole domain

What about Frege in Begriffsschrift, however? There’s nothing there explicit about domains. Is that because he thinks that the quantifiers are always to be taken as ranging, not over this or that domain, but over absolutely everything — over all objects that there are?

Some have taken this to be Frege’s view. In particular, when Dummett talks about Frege and unrestricted quantification in Frege: Philosophy of Language, he is firmly of the view that “When these individual variables are those of Frege’s symbolic language, then their domain is to be taken as simply the totality of all objects” (p. 529).

But it isn’t obvious to me that Frege is committed to an idea of absolutely general quantification, at least in Begriffsschrift. (Re)reading the appropriate bits of that book plus the two other contemporary pieces published in Bynum’s Conceptual Notation, and the two contemporary pieces in Posthumous Writings, there doesn’t seem to be a clear commitment to the view.

OK, Frege will write variations on: “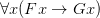” means that whatever you put in place of the “”, “” 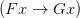is correct. But note that here he never gives daft instantiations of the variable, totally inappropriate to the e.g. arithmetic meaning of F and G.

This is not quite his example, but he does the equivalent of remarking that “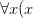 is even 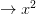is even)” isn’t refuted by “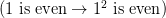” because (given the truth-table for “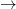”), that comes out true. But he never, as he should if the quantifiers are truly absolutely unrestricted, consider instances such as “The Eiffel Tower is even  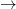The Eiffel Towe 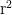is even” — which indeed is problematic as the consequent looks nonsense. (Has Frege committed himself in Begriffsschrift to the view that every function is defined for the whole universe?)

Similarly, in PW, p. 27, Frege cheerfully writes “The numbers … are subject to no conditions other than 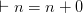, etc.”. There’s not a flicker of concern here about instances — as they would be if the implicit quantifier here were truly universal — such as “”. Rather it seems clear that here Frege’s quantifiers are intended to be running over … numbers!

(As a diverting aside, note that even if Frege had committed himself to the view that every function is defined for the whole universe by giving a default value to when one at least of X, Y is non-arithmetic, that really wouldn’t help here. For then 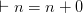taken as a quantification over everything would imply 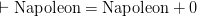and 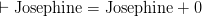and hence — since the right-hand sides take the default value– .)

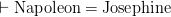Earlier in PW, p. 13, Frege talks about the concept script “supplementing the signs of mathematics with a formal element” to replace verbal language. And this connects with what has always struck me as one way of reading Begriffsschrift.

 Yes it is all purpose, in that the logical apparatus can be added to any suitable base language (the signs of mathematics, the signs of chemistry, etc. and as we get cleverer and unify more science, some more inclusive languages too). And then too we have the resources to do conceptual analysis using that apparatus (e.g. replace informal mathematical notions with precisely defined versions) — making it indeed a concept-script. But what the quantifiers, in any particular application, quantify over will depend on what the original language aimed to be about: for the original language of arithmetic or chemistry or whatever already had messy vernacular expressions of generality, which we are in the course of replacing by the concept script.
Yes, the quantifiers will then unrestrictedly quantify over all numbers, or all chemical whatnots, or …, whichever objects the base language from which we start aims to be about (or as we unify science, some more inclusive domain set by more inclusive language).
And yes, Frege’s explanation of the quantifiers — for the reasons Dummett spells out — requires us to have a realist conception of objects (from whichever domain) as objects which determinately satisfy or don’t satisfy a given predicate, even if we have no constructive way of identifying each particular object or of deciding which predicates they satisfy. Etc.

But the crucial Fregean ingredients (1) to (3) don’t add up to any kind of commitment to conceiving of the formalised quantifiers as absolutely unrestricted. He is, to be sure, inexplicit here — but it not obvious to me that a charitable reading of Begriffsschrift at any rate has to have Frege as treating his quantifiers as absolutely unrestricted.