Which is the quantifier?

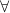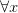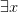A note on another of those bits of really elementary logic you don’t (re)think about from one year to the next – except when you are (re)writing an introductory text! This time, the question is which is the quantifier, ‘’ or ‘’, ‘’ or ‘’? Really exciting, eh?

Those among textbook writers calling the quantifier-symbols 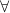’, ‘’ by themselves the quantifiers include Barwise/Etchemendy (I’m not sure how rigorously they stick to this, though). Tennant also calls e.g. ‘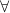’ a quantifier, and refers to  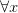‘’ as a quantifier prefix.

Those calling the quantifier-symbol-plus-variable the quantifier include Bergmann/Moor/Nelson, Chiswell/Hodges, Guttenplan, Jeffrey, Lemmon, Quine, Simpson, N. Smith, P. Smith, Teller, and Thomason. (Lemmon and Quine of course use the old notation ‘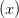’ for the universal quantifier.) Van Dalen starts by referring to ‘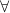’ as the quantifier, but slips later into referring to ‘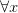’ as the quantifiers.

It’s clear what the majority practice is. Why not just go with it?

Modern practice is to parse ‘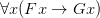’ as  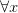‘’ applied to ‘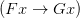’. However Frege (I’m reading through Dummett’s eyes, but I think this is right, mutating the necessary mutanda to allow for differences in notation) parses this as the operator we might temporarily symbolize ‘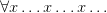’ applied to  ‘’.

To explain: Frege discerns in ‘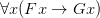’ the complex predicate ‘’ (what you get by starting from ‘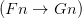’ and removing the name). Generalizing involves applying an operator to this complex predicate (it really is an ‘open sentence’ not in the sense of containing free variables but in containing gaps — it is unsaturated). Another way of putting it: for a Fregean, quantifying in is a single operation of taking something of syntactic category s/n, and forming a sentence by applying a single operation of category s/(s/n). This quantifying operator is expressed by filling-the-gaps-with-a-variable-and-prefixing-by- ‘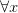’ in one go, so to speak. The semantically significally widget here is thus ‘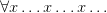’. Yes, within that, ‘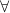’ is a semantically significant part (it tells us which kind of quantification is being done). But — the Fregean story will go — ‘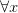’ is not a semantically significant unit.

So, whether you think ‘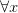’ is worthy of being called the universal quantifier is actually not such a trivial matter after all. For is ‘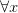’ a semantically significant unit? You might think that the true believing Fregean protests about this sort of thing too much. I’d disagree — but at any rate the underlying issue is surely not just to be waved away by unargued terminological fiat.