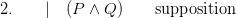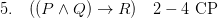Why mandatory reiteration in Fitch-style proofs?

Digressing from issues about the choice of language(s), another post about principles for selecting among natural deduction systems — another choice point, and (though I suppose relatively minor) one not considered by Pelletier and Hazen.

Take the most trite of examples. It’s agreed that if P then R. I need to convince someone that if P and Q then R (I’m dealing with a dullard here!). I patiently spell it out:

We are given if P then R. So just suppose that P and Q. Then of course P will be true, and hence (given what we agreed) R. So our supposition leads to R, OK? – hence as I said, if P and Q then R.

You want that set out more formally? Here goes, indenting sub-proofs Fitch-style!

Job done!

Except that in many official versions of Fitch-style proofs, this derivation is illegitimate. We can’t appeal to the initial premiss at (1) in order to draw the modus ponens inference inside the subproof: rather, we have to first re-iterate the premiss in the subproof, and then appeal to this reiterated conditional in applying modus ponens.

This requirement for explicit reiteration seems to go back to Jaśkowski’s first method of laying out proofs; and it is endorsed by Fitch’s crucial Symbolic Logic (1952). Here are some other texts using the same graphical layout as introduced by Fitch, and also requiring inferences in a subproof to appeal only to what’s in that subproof, so that we have to use a reiteration rule in order to pull in anything we need from outside the subproof: Thomason (1970), Simpson (1987/1999), Teller (1989).

Now, such a reiteration rule has to say what you can reiterate. For example: you can reiterate items that occur earlier outside the current subproof, so long as they do not appear in subproofs that have been closed off (and then, but only then, these reiterated items can be cited within the current subproof). But it is less complicated and seems more natural not to require wffs actually to be rewritten. The rule can then simply be: you can cite “from within a subproof, items that occur earlier outside the current subproof, so long as they do not appear in subproofs that have been closed off” — which is exactly how Barwise and Etchemendy (1991) put it. Others not requiring reiteration include Hurley (1982), Klenk (1983) and Gamut (1991). (Bergmann, Moor and Nelson (1980) have a rule they call reiteration, but they don’t require applying a reiteration rule before you can cite earlier wffs from outside a subproof.)

So: why require that you must, Fitch-style, reiterate-into-subproofs before you can cite  e.g. an initial premiss? What do we gain by insisting that we repeat wffs within a subproof before using them in that subproof?

It might be said that, with the repetitions, the subproofs are proofs (if we treat the reiterated wffs as new premisses). But that’s not quite right as in a Fitch-style proof it is required that the premisses be listed up front, not entered ambulando. So we’d have to re-arrange subproofs with the new supposition and the reiterated wffs all up front: and no one insists that we do that.

Anyway: at the moment I’m not seeing any compelling advantage for going with Fitch/Thomason/Simpson/Teller rather than with Barwise and Etchemendy and many others. Going the second way keeps things snappier yet doesn’t seem any more likely to engender student mistakes, does it? But has anyone any arguments for sticking with a reiteration requirement?