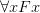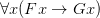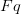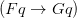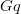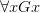The language(s) of first-order logic #1

In presenting a formal system of first-order logic, there are three major choice-points that concerning the language(s) we are going to be using.

Do we talk of one language or many languages (different languages for different interesting first-order theories, and different temporary ad hoc languages for use when we are regimenting different arguments)?
In explaining the semantics of quantifiers, do we give a Tarski-style account in terms of satisfaction (where we assign sequences of objects to sequences of variables)? Or do we make use of some new kind of supplementary names for objects in the domain, so that e.g. ‘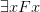’ comes out true on an interpretation if  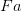‘’ is true for some extra name ‘a’ on some perhaps extended interpretation?
What do we use as parameters in natural deduction? Names? Variables? A new, syntactically differentiated, sort of symbol?

Here, the first issue is to some extent a matter of presentational style, but (as we will note in a subsequent post) the details of what you say can make a difference on more substantive points. The second issue is probably familiar enough and we needn’t delay over it just now. To elucidate the last issue, consider a natural deduction proof to warrant  the inference  ‘Everyone loves pizza. Anyone who loves pizza loves ice-cream. So everyone loves ice-cream’. The proof goes (maybe with extra bells and whistles, such as Fitch-style indentation, or maybe with rearrangement into a tree) like this:

Here, I’ve used the intentionally unusual ‘q’. But what would you prefer to write in its place? Some would use e.g. ‘x’, picked from the list of official variables for the relevant language in play.  Some would use e.g.  ‘a’, picked  from the list of official individual constants (names) for the relevant language. However, we might note that  ‘q’  is neither being used as a variable tied to a prefixed quantifier, nor used as a genuine constant naming a determinate thing, but in a third way. It is, as they say, being used as a parameter. So we might wonder whether we should somehow  mark syntactically when a symbol is being used as a parameter (following the Fregean precept that important semantic differences should be perspicuously marked in our symbolism).

It is interesting to see how different authors of logic textbooks for students which cover natural deduction handle our three choice-points. So let’s take a number of texts in turn, in the chronological order of editions that I can reach from my shelves.

Neil Tennant, Natural Logic (Edinburgh UP, 1978) talks of the language of first-order logic. In giving a model, distinguished names are assigned objects, but later “undistinguished names” are employed as names of arbitrary objects considered in the course of a proof — i.e. they are employed as parameters. Free variables feature not in proofs but in the syntactic story about how wffs are built up, and the associated Tarski-style semantic story for wffs.

Jon Barwise and John Etchemendy, The Language of First-Order Logic (CSLI, 2nd ed. 1991) talks initially of FOL, the language of first-order logic, but soon starts talking of first-order languages, plural. On semantics, there is initially a version of the idea that we extend a first-order language with additional names, and ‘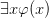’ is true on interpretation I so long as ‘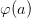’ is true on some extension of I which is just like I except in what it assigns to the new name ‘a’. But later, an official Tarskian story is given. Wffs with free variables are allowed, but don’t feature in proofs where parameters are all constants.

Merrie Bergmann, James Moor, Jack Nelson, The Logic Book (McGraw-Hill, 3rd ed. 1998) introduces a single, catch-all language PL. Initially, just a very informal semantics is given, enough for most purposes. But when a formal account is eventually given,  it is Tarskian. The authors allow free variables in wffs. But their natural deduction system is again presented as a system for deriving sentences from sentences, and in the course of proofs it is names (not free variables) which are used parametrically.

Dirk van Dalen, Logic and Structure (Springer, 4th ed. 2004) allows for many languages, different languages of different signatures. The book’s semantics is non-Tarskian, and goes via adding extra constant symbols, one for every element of the domain, and then ‘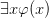’ is true on interpretation I so long as some ‘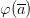’ is true (where ‘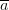’ is one of the extra constants). The natural deduction system uses free variables in a parametric role.

Ian Chiswell and Wilfrid Hodges, Mathematical Logic (OUP, 2007) allows many languages with different signatures. The authors give a straight Tarskian semantics. Their natural deduction system allows wffs with free variables, and allows both variables and constants to be used parametrically (what matters, of course, is that the parametrically used terms don’t appear in premisses which the reasoning relies on).

Nick Smith, Logic: The Laws of Truth (Princeton, 2012) goes for one all-encompassing language of FOL, with unlimited numbers of predicates of every arity etc. When we actually use the language, we’ll only be interested in a tiny fragment of the language, and interpretations need only be partial. Semantically, Smith is non-Tarskian: ‘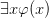’ is true on interpretation I so long as ‘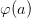’ is true on some extension of I which is just like I except in what it assigns to the new name  ‘a’. Smith’s main proof system is a tableau system; but he also describes a Fitch-style system and other ND systems. In these cases, names are used as parameters. (The one all-encompassing language of FOL will give us an unending supply.)  Smith allows free variables in wffs in his syntax — but these wffs don’t get a starring role in his proof systems.

So in summary we have, I think, the following (correct me if I have mis-assigned anyone, and let me know about other comparable-level texts which cover natural deduction if they are interestingly different):

Book
One/ Many?
Tarksi/non-Tarski?
Parameters?


Tennant
One
Tarski
Names


Barwise and Etchemendy
Many
Both
Names


Bergmann, et al.
One
Tarski
Names


van Dalen
Many
Non-Tarski
Variables


Chiswell and Hodges
Many
Tarski
Both


Smith
One
Non-Tarski
Names

The obvious question is: is there a principled reason (or at least a reason of accessibility-to-students) for preferring one selection of options over any other, or is it a matter of taste which way we go?

But first, in the next post, let’s take a look back at the approaches taken by some of the classics of logic on such matters. To be continued.