Empty domains #3 – from Vej Kse

The following was posted as a comment to Empty domains #1 by Vej Kse — but I think it is particularly interesting and worth highlighting as a stand-alone post. 

There is an elegant and natural (from a user’s perspective) way to allow empty domains, which has been known in categorical logic and modern type theories (based on de Bruijn’s Automath and Martin-Löf’s type theory) for over 40 years.

It consists in considering formulae only relative to a given context (list) of variables (which must contain all free variables of the formula, and can be empty if the formula is closed). In many-sorted logic, each variable is attributed a sort in the context. In a way, “standard” first-order logic (the one taught in most logic textbooks) amounts to working in a context with a countable number of variables.

In natural deduction for such a system, we want to prove a formula 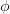in a variable context 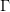from a list of formulae 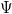(an hypothesis context), where all involved formulae are well-formed in the context 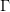. Just like proving an implication in a given hypothesis context amounts to proving the consequent from the context expanded with the antecedent (the variable context hold fixed), proving a universal quantification 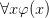in a variable context amounts to proving 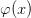in the context expanded with (the hypothesis context hold fixed).

The main reason of using a variable context, in my view, is not that it allows empty domains, but that it models more faithfully how mathematicians reason. We do not start our informal proofs by assuming given a countable sequence of variables of our domains of interest; when we write proofs, variable introduction parallels hypothesis introduction: “Let x be a real number …” vs. “Let’s assume the axiom of choice.”. Moreover, mathematicians remember just as well the variables they introduced (stored in the “variable context” part of their memory) as they remember the hypotheses they introduced (stored in the “hypothesis context” part of their memory). “Standard” first-order logic fails to model that memory of the variables introduced.

The standard proof in “standard” first-order logic of 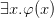from 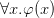is odd for mathematicians precisely because a variable appears out of nowhere, without ever being introduced.

1. Let’s assume ;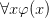

2. Eliminate 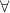by applying it at 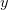, which gives us .

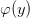3. Introduce 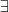, which gives us .

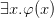In correcting a student’s work I would write in red next to the second step: “what is this 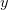? you never introduced it”. The proof should introduce the variable 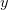before using it, which also means that it cannot just be forgotten at the end of the proof, even though it doesn’t appear in the conclusion (it’s still in the memory of the reader). To remove it from the context, a 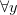must be added, giving .

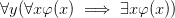Advantages of working with variable contexts besides allowing empty domains and being more faithful to ordinary reasoning:

– Leaner semantics: No need to assign values to infinitely many unused variables; we only have to assign values to the variables in the finite context.

– Separation of concerns: The quantifier rules don’t have side-conditions any more, these become well-formedness conditions on the contexts (all variable names must be different so that, when a context is extended, the name must be new) and the formulae (they must be well-formed in the contexts in which they are used, in particular only contain variable names present in those contexts).

– The structure of the quantifier introduction and elimination rules is more transparent: it takes the form of an adjunction, like for the other connectives.

– It repairs the symmetry between assumptions and variables, implication and universal quantification, conjunction and existential quantification (broken by their very different treatments in “standard” first-order logic), paving the way to the propositions-as-types (Curry-Howard) correspondence and modern type theories.

Disadvantages:

– Prenex normal forms depend on the inhabitedness assumption (and the law of excluded middle) (so we can still use it in Peano arithmetic for instance, just not in general first-order logic).

– The weight of tradition.

Here are a few books in which first-order logic is presented using variable contexts:

– Peter T. Johnstone: “Sketches of an elephant: A topos theory compendium” (Chapter D1);

– Bart Jacobs: “Categorical logic and type theory” (Chapter 4);

– Paul Taylor: “Practical foundations of mathematics” (Section 1.5);

– Richard Bornat: “Proof and disproof in formal logic: An introduction for programmers”.