Empty domains #1
From wild mathematical universes back to nothing much at all: the question of empty domains in first-order logic. Not that I have anything very insightful to say: but I want to get my mind clearer before committing myself to a line in IFL2.
In his nice book Logic (1977), Wilfrid Hodges introduces a tableau system with the following four rules for dealing with quantifiers. Two rules allow us to push a negation past a quantifier — so given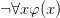 
on a branch you add 
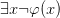, and dually. Then the rules for dealing with bare quantifiers are as follows. Given 
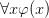on a branch, you can add 
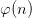for any 
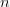already featured on the branch. While given 
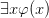on a branch, you can add 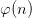for some 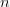which is not already used on the branch.
Compared with the standard rules for tableaux as in e.g. Jeffrey’s Formal Logic: Its Scope and Limits (1967/1981), Hodges’s quantifier instantiation rules are a tad neater, indeed elegantly symmetric — simply: instantiate universals with old names, existentials with new names. There’s a price to pay, though. Using ‘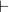
’ for provability in Hodges’s system, we notably do not get 
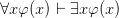. But that is all to the good, Hodges thinks. That inference fails if we allow the empty domain. “Many logicians add one further derivation rule, which has the effect of decreeing that every domain of quantification has at least one individual in it. From our point of view this would be a mistake. A domain of quantification can perfectly well be empty — as it well may be if the conversation turns to discussing intelligent life on other planets.”
At first blush this is very neat — a more inclusive logic and more elegant rules. What’s not to like. But on second thoughts, there are serious problems. As David Bostock points out in his Intermediate Logic (OUP 1997), in Hodges’s system we do get e.g.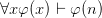 
and 
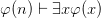so transitivity of derivability fails; and there are other nasty effects. Such consequences do seem pretty unhappy. Bostock diagnoses the source of the trouble to be Hodges’s half-way-house position of wanting to accommodate empty domains while his logic requires that names have denotations. Allow empty names too and of course both 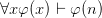and 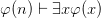fail, and transitivity can be restored.
And indeed, leaving aside nasty effects like transitivity failure, it is difficult to see why it should be a desirable feature of a logic that it allows empty domains but not empty names. After all, if “the conversation turns to discussing intelligent life on other planets” it could equally (back in the nineteenth century) turn to discussing the intramercurial planet Vulcan, or (later) turn to discussing Ern Malley (among poets) or Nat Tate (among painters) or Frederick R. Ewing (among novelists). And if our logic has functions, then we can find ourselves unwittingly discussing partial functions so using more terms which fail to have references. If we want to avoid the mishap of talking of things that don’t exist, then surely we’ll want to avoid not just wholesale foul-ups (empty domains) but local foul-ups (empty terms). If we push Hodges’s rationale for allowing empty domains to its natural conclusion, then, it seems that seems we have to go the full revisionary hog and be free logicians. But free logics — while not horrendous — haven’t the elegant simplicity of Hodges’s system. Do we really have to end up there? Not in an introductory book, that’s for sure! To be continued …
Footnote: what is the natural deduction analogue of Hodges’s system? I think this works: take the usual sort of 
-elimination rule (given 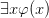start a subproof w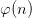ith with 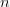new …), let the 
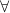-elimination rule allow just instantiation with respect to names already appearing (not in finished subproofs), and add the two rules, from 
infer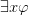 
and its dual. But I guess this isn’t an entirely natural presentation of a natural deduction system, if we like thinking Gentzen-style of introduction rules as more fundamental, as meaning-fixing, and elimination rules to be justified as being in harmony with them.
