Pi and the Golden Ratio

Two of my favorite numbers are pi:

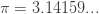
and the golden ratio:

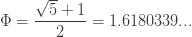
They’re related:

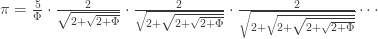
Greg Egan and I came up with this formula last weekend. It’s probably not new, and it certainly wouldn’t surprise experts, but it’s still fun coming up with a formula like this. Let me explain how we did it.

History has a fractal texture. It’s not exactly self-similar, but the closer you look at any incident, the more fine-grained detail you see. The simplified stories we learn about the history of math and phy...