Frege on “if”

I’ve been looking at the passage early in the Begriffsschrift where Frege introduces the material conditional — not, of course, using that label, and not of course with our notation. He notes that 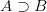can be affirmed when A is denied or when B is affirmed, and in those cases “there need not exist a causal connection between the two contents” (the content of A and the content of B). One can also

make the judgment without knowing whether A and B are to be affirmed or denied. For example, let A denote the circumstance that the Moon is in quadrature [with the sun] and B the circumstance that it appears as a semicircle. In this case  can be translated with the aid of the connective ‘if’: ‘If the moon is in quadrature, then it appears as a semicircle’. The causal link implicit in the word ‘if’, however, is not expressed by our symbols, although a judgement of this kind can be made only on the basis of such a link.

That’s Michael Beaney’s translation, with notation changed: but other translations don’t differ in relevant ways. In particular, they all use the word ‘causal’ in rendering Frege’s remarks. And this is what caught my eye.

For Frege seems to be intending to make general claims here. To judge 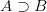  we need not suppose that there is a causal connection or link between A and B, it suffices (of course) to be in a position to deny A or assert B. By contrast, however, a judgement if A then B can only be made on the basis of a causal link. And doesn’t that strike us as an odd line for him to take, given that Frege’s first interest is in the language of arithmetic and the  language of analysis, where causation doesn’t come into it? True arithmetical ‘if’s aren’t causal ‘if’s — or so many of us English-speaking analytic philosophers would be inclined to say (not least because we have read our Frege!).

We might wonder, then about the shared translation here. But the relevant German is “ursächlicher Zusammenhang” and “ursächliche Verknüpfung”; and according to the dictionary ‘ursächlich’ means ‘causal’. So it seems that the translations are right.

Though this sets me musing. In English (or at least, in my corrupted-by-philosophy English) there is something of a disconnect between ‘cause’ and ‘because’. If we have A true and this fact causes B to be true, then I am happy to say B, because A. But this doesn’t reverse: in particular, in mathematical cases where  I am happy to say something of the form B, because A, I’d usually balk at talking about causation. For example, I’m quite happy to say of a particular function that it is computable because it is primitive recursive, but would balk (wouldn’t you?) at saying that its being primitive recursive causes it to be computable.

Now I suppose English could have had the notion of becausal link, more general than a causal connection, i.e. some connection or other that holds when B, because A is true. And then we could imagine the view that “a becausal link is implicit in the word ‘if'” (however exactly we are to spell out ‘implicit’ here).

So that raises a question: when Frege talks about ‘if’s and causal connections, does he in fact mean anything stronger than becausal connections (assuming that a ‘because’ need not be causal ‘because’). How are things in philosophical German? Does “ursächliche Verknüpfung” definitely connote a causal as opposed to, more generally, becausal link?