Large Countable Ordinals (Part 2)

Last time I took you on a road trip to infinity. We zipped past a bunch of countable ordinals

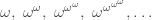
and stopped for gas at the first one after all these. It’s called Heuristically, you can imagine it like this:

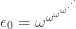
More rigorously, it’s the smallest ordinal obeying the equation

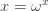
Beyond εo

But I’m sure you have a question. What comes after ?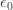

Well, duh! It’s

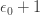
Then comes

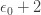
and then eventually we get to

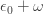
and then

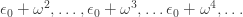
and after a long time

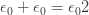
and then eventually

and then eventually….

Oh, I see! You wanted...