Shelves and the Infinite

A shelf is a set with a binary operation 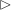that distributes over itself:

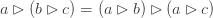
There are lots of examples, the simplest being any group, where we define

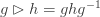
They have a nice connection to knot theory, which you can see here if you think hard:

My former student Alissa Crans, who invented the term ‘shelf’, has written a lot about them, starting here:

• Alissa Crans, Lie 2-Algebras, Chapter 3.1: Shelves, Racks, Spindles and Quandles, Ph.D. thesis, U.C. Riverside, 2004.

I could tell you a long and entert...