The Capricornoid

This curve is called a capricornoid, because it’s supposed to resemble the sign of Capricorn in the zodiac, though I don’t see how. Its equation is

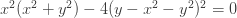
so it’s described by a quartic equation in two variables.

What makes this curve fun is that it has two different kinds of singularities. At the point

it has a tacnode, meaning that two different branches of the curve are tangent at that point. More precisely, two different circles kiss the curve at that point.

Further up, at the point

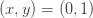
there is...