Peter Smith's Blog, page 28
October 13, 2022
GWT2, Category theory, and other delights …
A last call for comments/corrections (please!!) for the draft second edition of Gödel Without Tears — I plan to finalize and publish a paperback version around the end of the month. You can download the draft here (though I imagine that anyone interested will have done so by now).
I’ve mentioned before that my three hundred pages of introductory notes on category theory are downloaded surprisingly often — frequently enough for it to be rather embarrassing, given their current ramshackle state. So, with GWT2 simmering on the back burner while I wait to see if there are any last minute suggestions to deal with, I’m getting back to thinking a bit about categories.
I was, for a while, stumbling over two things when thinking about how to revise/develop the notes. Firstly, I didn’t have a clear enough conception of where I wanted to get to. Secondly, I’ve become increasingly unhappy with the way the very opening chapters are handled (with those distracting sermons about set theory!). But I think that things are now falling into place rather better.
On the question of scope, of where to finish, I’m lowering my sights a bit. I had occasion, the other day, to be looking at the classic book on topos theory by Mac Lane and Moerdijk. It starts with a scene-setting fourteen pages of “Categorical Preliminaries” — a glorified checklist of what you need to bring to the party if you are planning to dive into the book. And that checklist more or less exactly corresponds to the topics sort-of covered (in rushed way towards the end) in the existing notes. So that’s persuaded me that maybe, after all, the notes do get to a sensible enough stopping point (and perhaps only need be rounded out with some brief pointers to routes onwards).
And on the question of how to start, I’ve decided that fussing at the outset about such issues as whether we should identify functions with their graphs just doesn’t make for a happy beginning. That’s largely got to go! But this makes for quite a bit of fiddly re-writing over the initial chapters.
I’m having a family break for a couple of weeks, so the new version of the first seventeen chapters or so won’t be ready for a few weeks. But I’m feeling decidedly cheerier about the project of improving those notes, at least enough for me to rest fairly content with the unambitious result.
The wider world continues to go mad and/or bad in various depressing ways. The most distractingly enjoyable novel I have read just recently? Perhaps Elspeth Barker’s atmospherically gothic O Caledonia. I dived in because of an enthusiastic recommendation by Maggie O’Farrell. I enthusiastically pass on the recommendation!
I have also been much distracted by Edmund de Waal’s The White Road, swept along by his obsession with porcelain and its origins (with walk on parts for Spinoza and Leibniz by the way). Strangely gripping I find!
The post GWT2, Category theory, and other delights … appeared first on Logic Matters.
September 30, 2022
Avigad on Mathematical Logic and Computation
 A heads up, as they say. Jeremy Avigad’s new book Mathematical Logic and Computation has now been published by CUP (or at least, an e-version is already available on the Cambridge Core system if you have access — with the hardback due soon). Here’s a link to the front matter of the book, which gives you the Table of Contents and the Preface. Between them, they give you a fair idea of the coverage of the book.
A heads up, as they say. Jeremy Avigad’s new book Mathematical Logic and Computation has now been published by CUP (or at least, an e-version is already available on the Cambridge Core system if you have access — with the hardback due soon). Here’s a link to the front matter of the book, which gives you the Table of Contents and the Preface. Between them, they give you a fair idea of the coverage of the book.
As you’d expect from this author, this book is very worth having, an excellent addition to the literature, with plenty more than enough divergences and side-steps from the more well-trodden paths through the material to be consistently interesting. Having quickly read a few chapters, and dipped into a few more, I’d say that the treatments of topics, though very clear, are often rather on the challenging side (Avigad’s Carnegie Mellon gets very high-flying students in this area!). For example, the chapters on FOL would probably be best tackled by someone who has already done a course based on something like Enderton’s classic text. But that’s not a complaint, just an indication of the level of approach.
When the physical version becomes available — so much easier to navigate! — I’m going to enjoy settling down to a careful read through, and maybe will comment in more detail here. Meanwhile, this is most certainly a book to make sure your library gets.
The post Avigad on Mathematical Logic and Computation appeared first on Logic Matters.
September 25, 2022
Hilary Mantel, 1952–2022
 From a photo by Richard Phibbs for Harper’s Bazaar, taken at Hampton Court Palace.
From a photo by Richard Phibbs for Harper’s Bazaar, taken at Hampton Court Palace.Such a wonderful writer. The Wolf Hall trilogy is the extraordinary work of our times, that only strikes you as all the greater on rereading. And the many touching tributes to Hilary Mantel’s human qualities make her untimely death seem all the sadder.
The post Hilary Mantel, 1952–2022 appeared first on Logic Matters.
September 23, 2022
Another book, another disappointment
 I picked up a copy of the very recently published A New History of Greek Mathematics by Reviel Netz in the CUP Bookshop a couple of weeks ago — an impulse buy, encouraged by the rave endorsements on the back cover.
I picked up a copy of the very recently published A New History of Greek Mathematics by Reviel Netz in the CUP Bookshop a couple of weeks ago — an impulse buy, encouraged by the rave endorsements on the back cover.
This is the most irritating book I’ve read (well, not read to the bitter end) for a long time. On the positive side, it is extraordinarily interesting and illuminating about the intellectual and cultural milieus at various stages in the development of mathematics in the ancient Greek world. It told me a great deal about our fragmentary knowledge about the earlier figures, about the kinds of mathematics being pursued, when and why. That background story is told very readably, with zest and engaging enthusiasm. So Geoffrey Lloyd could be spot on when he writes that the book “brings to bear an extraordinary range of material from non-Greek as well as Greek sources, and develops original arguments concerning the fundamental question of why and how Western science developed in the way it did”.
So why the irritation, the great disappointment? Because the author, sad to say, gives no sense at all of having any real feel for mathematics. His accounts of ancient proofs (and actually there are surprisingly few detailed ones) are to my mind uniformly very poorly and unclearly done; they just don’t pass muster by normal expositional standards. I suspect that the author has zero significant mathematical background: and it shows badly. Having — only metaphorically, as I hate maltreating books! — thrown the New History across the room for the fourth or fifth time in frustration, I gave up after Archimedes. Though I took away this much: one day, I’d like to find out more about just what Archimedes knew about conics and the proofs he had available to him, as reconstructed by a competent mathematician.
The post Another book, another disappointment appeared first on Logic Matters.
September 22, 2022
GWT2 — a third (near-final?) full draft
 There is now a third complete draft of the forthcoming new edition of Gödel Without (Too Many) Tears. You can download it here.
There is now a third complete draft of the forthcoming new edition of Gödel Without (Too Many) Tears. You can download it here.
What’s changed this time, since the last full draft? There has been some more typographical micro-adjusting (you won’t notice!). A few more typos have been fixed, and there have been some scattered very minor changes in phrasing for clarity’s sake. I plan to do a bit more work on the index, but I hope the rest of the book is now in a near-final state.
Corrections and suggestions for local improvements will still be extremely welcome for another few weeks. I’ll then be getting back to GWT after a planned holiday and family time. To be definite: I’ll be calling a halt to further tinkering the weekend of October 29th, with the aim of getting a second edition out in print in November. So all comments, including — especially including! — quick notes of the most trivial typos, will be most welcome until then. (And many thanks to those who have emailed comments so far.)
The post GWT2 — a third (near-final?) full draft appeared first on Logic Matters.
September 17, 2022
Saul Kripke, 1940–2022
Much will be written, no doubt, about the man (whom I never met), and here I remember only the impact that Kripke had on logic-minded philosophers of my generation and the next. That was immense, from the time of his absurdly precocious first papers on modal logic (the first JSL paper published when he was nineteen), through the 1970 Princeton lectures on Naming and Necessity, and the later 1970s papers — such as the “Outline of a Theory of Truth”. And there was so much more too. Those 1970s papers struck me, still strike me, as a paradigm of philosophy — imaginative but full of good sense and straight talk, with forceful arguments appealingly written with great clarity, and in the background a real depth of technical logical knowledge lightly worn.
Unlike some, I wasn’t such a fan of Kripke’s 1981 long paper on Wittgenstein and rule-following, which indeed perhaps marked the end of his extraordinarily fertile great publishing period. But there is a great deal of unpublished work from then and later, with significant pieces to appear in further volumes of his Collected Papers if the first volume, Philosophical Troubles, is anything to go by. I look forward to that. And look back to so many rich hours spent in Kripke’s intellectual company.
The post Saul Kripke, 1940–2022 appeared first on Logic Matters.
September 15, 2022
Postcard from Cambridge to … Bulgaria
 Wren Library, Trinity College Cambridge
Wren Library, Trinity College CambridgeAs I have said before, it is difficult to know quite what to make of the absolute numbers given in the stats for this website (supposedly there about 35K ‘unique visitors’ a month). But the relative numbers can surely be trusted. Every month, the largest number of visitors come from the US, followed by Germany and then GB. And there are no surprises in the next few countries down the list.
But regularly about the tenth on the list, ordered by numbers of page views, is Bulgaria. And this really is a surprise, at least to me. The population of that country is less than a fifth of that of Poland, for example, yet supplies a dozen times as many visitors. Indeed, there are over a quarter as many visitors from Bulgaria as from here in GB. In fact, relative to size, it seems that’s where Logic Matters is most read!
A little googling suggests that logic has a very substantial presence in the University of Sofia, with a large department. So maybe some students from there find their way here. And I guess free resources are always going to be particularly appreciated by those in relatively poorer countries. Anyway, warm greetings from Cambridge, if you are exploring Logic Matters from Bulgaria!
The post Postcard from Cambridge to … Bulgaria appeared first on Logic Matters.
September 14, 2022
GWT2 — a second full draft
 There is now a second complete draft of the forthcoming new edition of Gödel Without (Too Many) Tears. You can download it here.
There is now a second complete draft of the forthcoming new edition of Gödel Without (Too Many) Tears. You can download it here.
What’s changed? There has been a fair bit of typographical tidying (which you no doubt won’t notice, but I might as well try to make things consistent!). The index has grown a bit, though there is more work to be done there. Some typos have been removed, there have been some scattered minor changes in phrasing, and further changes to tidy the way topics in different chapters are linked together. But the main update has been to the chapter on the Diagonalization Lemma: I’ve hopefully much improved this by re-arranging the material in a more logical way.
So that’s enough by way of updating to be worth putting on line now. The first full draft has been downloaded about 650 times. If you are one of those actually reading it, you might want to download the new improved version.
To repeat what I said before: It is too late to write a very different book, and after all this is supposed to be just a revised edition of the seemingly quite well-liked GWT1! This is not the moment, then, for radical revisions. But otherwise, all suggestions, comments and corrections, including quick notes of the most trivial typos, will be most welcome! Send to the e-mail address on the first page of PDF, or comment here. (Just note the date of the version you are commenting on.) Comments will continue to be welcome for the next month or so.
The post GWT2 — a second full draft appeared first on Logic Matters.
September 8, 2022
In the midst of life …
The post In the midst of life … appeared first on Logic Matters.
September 6, 2022
The Annotated Gödel
 Some years ago, Charles Petzold published his The Annotated Turing which, as its subtitle tells us, provides a guided tour through Alan Turing’s epoch-making 1936 paper. I was prompted at the time to wonder about putting together a similar book, with an English version of Gödel’s 1931 paper interspersed with explanatory comments and asides. But I thought I foresaw too many problems. For a start, not having any German, I’d have had to use one of the existing translations, which would lead to copyright issues, and presumably extra problems if I wanted to depart from the adopted translation by e.g. rendering Bew by Prov, etc. And then I felt it wouldn’t be at all easy to find a happy level at which to pitch the commentary.
Some years ago, Charles Petzold published his The Annotated Turing which, as its subtitle tells us, provides a guided tour through Alan Turing’s epoch-making 1936 paper. I was prompted at the time to wonder about putting together a similar book, with an English version of Gödel’s 1931 paper interspersed with explanatory comments and asides. But I thought I foresaw too many problems. For a start, not having any German, I’d have had to use one of the existing translations, which would lead to copyright issues, and presumably extra problems if I wanted to depart from the adopted translation by e.g. rendering Bew by Prov, etc. And then I felt it wouldn’t be at all easy to find a happy level at which to pitch the commentary.
Plan (A) would be to follow Petzold, who is very expansive and wide ranging about Turing’s life and times, and is aiming for a fairly wide readership too (his book is over 370 pages long). I wasn’t much tempted to try to emulate that.
Plan (B) would be write for a much narrower audience, readers who are already familiar with some standard modern textbook treatment of Gödelian incompleteness and who want to find out how, by comparison, the original 1931 paper did things. You then wouldn’t need to spend time explaining e.g. the very ideas of primitive recursive functions or Gödel numberings, but could rapidly get down to note the quirks in the original paper, giving a helping hand to the logically ept so that they can navigate through. However, the Introductory Note to the paper in the Collected Works pretty much does that job. OK, you could say a bit more (25 pages, perhaps rather than 14). But actually the original paper is more than clear enough for that to be hardly necessary, if you have already tackled a good modern treatment and then read that Introductory Note for guidance in reading Gödel himself.
Plan (C) would take a middle course. Not ranging very widely, sticking close to Gödel’s text. But also not assuming much logical background or any prior acquaintance with the incompleteness theorems, so having to slow down to explain ideas of formal systems, primitive recursion and so on and so forth. But to be frank, I didn’t and don’t think Gödel’s original paper is the best peg on which to hang a first introduction to the incompleteness theorems. Better to write a book like GWT! So eventually I did just that, and dropped any thought of doing for Gödel something like Petzold’s job on Turing.
But now, someone has bravely taken on that project. Hal Prince, a retired software engineer, has written The Annotated Gödel, a sensibly-sized book of some a hundred and eighty pages, self-published on Amazon. Prince has retranslated the incompleteness paper in a somewhat more relaxed style than the version in the Collected Works, interleaving commentary intended for those with relatively little prior exposure to logic. So he has adopted plan (C). And the thing to say immediately — before your heart sinks, thinking of the dire quality of some amateur writings on Gödel! — is that the book does look entirely respectable!
Actually, I shouldn’t have put it quite like that, because I do have my reservations about the typographical look of the book! Portions of different lengths of a translation from the 1931 paper are set in pale grey panels, separated by episodes of commentary. And Prince has taken the decidedly odd decision not to allow the grey textboxes containing the translation to split themselves over pages. This means that an episode of commentary can often finish halfway down the page, leaving blank inches before the translation continues in a box at the top of the next page. And there are other typographical choices while also quite unfortunately make for a somewhat unprofessional look. That’s a real pity, and does give a quite misleading impression of the quality of the book.
Now, I haven’t read the book with a beady eye from cover to cover; but the translation of the prose seems quite acceptable to me. Sometimes Prince seems to stick a bit closer to the Gödel’s original German than the version in the Works, sometimes it is the other way about. For example, in the first paragraph of Gödel’s §2, we have
G, undefinierten Grundbegriff: W, primitive notion: P, undefined basic notion,
while in the very next sentence we have
G, Die Grundzeichen: W, The primitive signs: P, The symbols.
But these differences are relatively minor.
Where P’s translation of G departs most is not in rendering the German prose but in handling symbolism. W just repeats on the Englished pages exactly the symbolism that is in the reprint of G on the opposite page. But where G and W both e.g. have “Bew(x)”, P has “isProv(x)”. There’s a double change then. First, P has rendered the original “Bew”, which abbreviated “beweisbare Formel”, to match his translation for the latter, i.e. “provable formula”. Perhaps a good move. But Prince has also included an “is” (to indicate that what we have here is an expression attributing a property, not a function expression). To my mind, this makes for a bit of unnecessary clutter here and elsewhere: you don’t need to be explicitly reminded on every use that e.g. “Prov” expresses a property, not a function.
Elsewhere the renditions of symbolism depart further. For example, G has “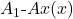 ” for the wff which says that
” for the wff which says that 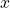 is an instance of Axiom Schema II.1. P has “isAxIIPt1(x)”. And there’s a lot more of this sort of thing which makes for some very unwieldy symbolic expressions that I don’t find particularly readable.
is an instance of Axiom Schema II.1. P has “isAxIIPt1(x)”. And there’s a lot more of this sort of thing which makes for some very unwieldy symbolic expressions that I don’t find particularly readable.
There are other debatable symbolic choices too. P has “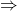 ” for the object language conditional, which is an unfortunate and unnecessary change. And P writes “
” for the object language conditional, which is an unfortunate and unnecessary change. And P writes “![x[v \leftarrow y]](https://i.gr-assets.com/images/S/compressed.photo.goodreads.com/hostedimages/1662534973i/33357118.png) ” for the result of substituting
” for the result of substituting 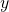 for
for  where
where  is free in
is free in 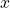 . This may be a compsci notation, but to my untutored eyes makes for mess (and I’d say bad policy too to have arrows in different directions meaning such different things).
. This may be a compsci notation, but to my untutored eyes makes for mess (and I’d say bad policy too to have arrows in different directions meaning such different things).
Other choices for rendering symbolism involve more significant departures from G’s original but are also arguably happier (let’s not pause to wonder what counts as faithful enough translation!). For example, there is a moment when G has the mysterious “p = 17 Gen q”: P writes instead “p = forall(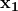 , q)”. In G, 17 is the Gödel number for the variable
, q)”. In G, 17 is the Gödel number for the variable 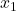 : P uses a convention of bolding a variable to give its Gödel number, which is tolerably neat.
: P uses a convention of bolding a variable to give its Gödel number, which is tolerably neat.
There’s more to be said, but I think your overall verdict on the translation element of Prince’s book might go either way. The prose is as far as I can judge handled well. The symbolism is tinkered with in a way which makes it potentially clearer on the small scale, but makes for some off-putting longwindedness when rendering long formulas. If you are going to depart from Gödel’s symbolism, you could be snappier. But as they say, you pays your money and makes your choice.
But what about the bulk of the book, the commentary and explanations interspersed with the translation of Gödel’s original? My first impression is definitely positive (as I said, I haven’t yet done a close reading of the whole). We do get a lot of helpful framing of the kind e.g. “Gödel is next going to define … It is easier to understand these definitions if we think about what he needs and where he is going.” And Prince’s discussions as we go along do strike me as consistently sensible, accurate, and will indeed be helpful to those who bring the right amount to the party.
I put it like that because, although I think the book is intended for those with little background in logic, I really do wonder whether e.g. the twenty pages on the proof of Gödel’s key Theorem VI will gel with those who haven’t previously encountered an exposition of the main ideas in one of the standard textbooks. This is the very difficulty I foresaw in pursuing plan (C). Most readers without much background will be better off reading a modern textbook. But, on the other hand, for those who have already read GWT (to pick an example at random!), i.e. those who already know something of Gödelian incompleteness, they should find this a useful companion if they want to delve into the original 1931 paper — though some of the exposition will now probably be unnecessarily laboured for them, while they would have welcomed some more “compare and contrast” explanations bringing out more explicitly how Gödel’s original relates to standard modern presentations.
In short, then: if someone with a bit of background does want to study Gödel’s original paper, whereas previously I’d just say ‘read the paper together with its Introductory Note in the Collected Works’, I’d now add ‘and, while still doing that, and depending quite where you are coming from and where you stumble, you might very well find some or even all of the commentary in Hal Prince’s The Annotated Gödel pretty helpful’.
The post The Annotated Gödel appeared first on Logic Matters.



