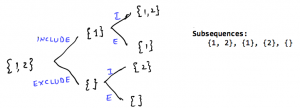Kamal Rawat's Blog

Logger Rate Limiter Solution (LeetCode)

This question is from the LeetCode Challenge (Aug-2020). See the original question here

Design a logger system that receive a stream of messages along with its timestamps, each message should be printed if and only if it is not printed in the last 10 seconds.

Given a message and a timestamp (in seconds granularity), return true if the message should be printed in the given timestamp, otherwise returns false.

It is possible that several messages arrive roughly at the same time.

Logger logger = new Logger();

// logging string "foo" at timestamp 1
logger.shouldPrintMessage(1, "foo"); returns true;

// logging string "bar" at timestamp 2
logger.shouldPrintMessage(2,"bar"); returns true;

// logging string "foo" at timestamp 3
logger.shouldPrintMessage(3,"foo"); returns false;

// logging string "bar" at timestamp 8
logger.shouldPrintMessage(8,"bar"); returns false;

// logging string "foo" at timestamp 10
logger.shouldPrintMessage(10,"foo"); returns false;

// logging string "foo" at timestamp 11
logger.shouldPrintMessage(11,"foo"); returns true;

The template of the solution (Logger class) should have the following APIs.

class Logger {

HashMap hash;

/** Initialize your data structure here. */
public Logger() {
hash = new HashMap();
}

/** Returns true if the message should be printed in the given timestamp, otherwise returns false.
If this method returns false, the message will not be printed.
The timestamp is in seconds granularity. */
public boolean shouldPrintMessage(int timestamp, String message) {
Integer prevTime = hash.get(message);
if(prevTime == null || (timestamp - prevTime >= 10) )
{
hash.put(message, timestamp);
return true;
}
return false;
}
}

/**
* Your Logger object will be instantiated and called as such:
* Logger obj = new Logger();
* boolean param_1 = obj.shouldPrintMessage(timestamp,message);
*/

Solution:

For each of the string that the Logger file receives, it need to keep a track of the last time this string was logged. This log-time is an integer value. So, we need to store one integer value for each of the string that we are receiving. A HashMap is a good data structure to store a pair.

Following is the solution for the given question:

class Logger {

HashMap hash;

/** Initialize your data structure here. */
public Logger() {
hash = new HashMap();
}

/** Returns true if the message should be printed in the given timestamp, otherwise returns false.
If this method returns false, the message will not be printed.
The timestamp is in seconds granularity. */
public boolean shouldPrintMessage(int timestamp, String message) {
Integer prevTime = hash.get(message);
if(prevTime == null || (timestamp - prevTime >= 10) )
{
hash.put(message, timestamp);
return true;
}
return false;
}
}

The time complexity of shouldPrintMessage function is constant.

Fitting Shelves Problem

Given the length of a wall w and infinite shelves of two lengths small and large (large > small).

Find the optimal solution to put the shelves in the wall such that the empty space left is minimum. We have to use the large shelves as much as possible (keeping the empty space minimum) because the large shelves are cheaper than the smaller ones.

Example:
Input: WallLength = 24 smallShelfLength = 3 largeShelfLength = 5
Output: S: 3 L: 3 E: 0

Explanation:
We use three units of both large and small shelves and 0 space is left empty.
3 * 3 3 * 5 = 24

Empty space = 0

Another solution could have been S: 8 L: 0 E: 0
but because the larger shelf is cheaper the previous solution should be the answer.

Solution:

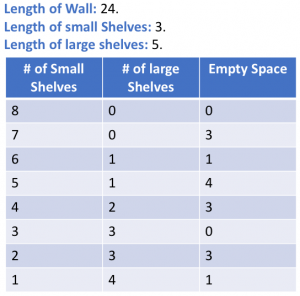
A simple solution is to try all possible combinations of small and large shelves.

Start by putting the maximum number of small shelves (with zero large shelves)
Keep reducing the number of small shelves and try to fit the maximum number of large shelves possible in the extra space.

The final answer is (3, 3, 0). 3 small Shelves, 3 large shelves and zero empty.

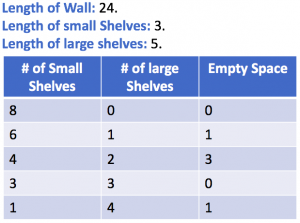
We can improve this brute-force way by increasing the number of large shelves in each iteration. So the number of rows in the above diagram will reduce:

The code for this is very simple as below:

Code:

void fittingShelves(int wall, int small, int large)
{
if(wall < small)
{
cout<< wall)
break;
int extra = wall - (numLarge * large);
// TRY TO PUT AS MANY SMALL AS POSSIBLE.
int numSmall = extra/small;
int empty = extra % small;
if(empty <<<<<<<

Output:

S:3 L:3 E:0
S:6 L:0 E:0
S:2 L:0 E:1
S:0 L:3 E:2

Assign Mice to Holes

There are N Mice and N holes placed in a straight line. Each hole can accommodate only 1 mouse.

A mouse can stay at his position, move one step right from x to x + 1, or move one step left from x to x − 1. Any of these moves consume 1 minute.

Assign mice to holes so that the time when the last mouse gets inside a hole is minimized.

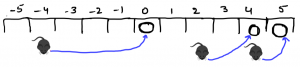
For example, Let the positions of mice are: 4 -4 2

positions of holes are: 4 0 5

Assign mouse at position x=4 to hole at position x=4 : Time taken is 0 minutes
Assign mouse at position x=-4 to hole at position x=0 : Time taken is 4 minutes
Assign mouse at position x=2 to hole at position x=5 : Time taken is 3 minutes
After 4 minutes all of the mice are in the holes.

Note that this may not be the only solution. With the same answer (4 min), there may exist multiple solutions. Another solution is as below:

Assign mouse at position x=4 to hole at position x=5 : Time taken is 1 minutes
Assign mouse at position x=-4 to hole at position x=0 : Time taken is 4 minutes
Assign mouse at position x=2 to hole at position x=4 : Time taken is 2 minutes
After 4 minutes all of the mice are in the holes.

Solution:

This problem can be solved using a Greedy Approach.

We put every mouse to its nearest hole to minimize the time. To do this, sort the positions of mice and holes and put the ith mice in the ith hole in the holes list.

While moving the mouse, keep a track of the maximum distance any mouse have moved.

Code:

int miceInHole(int[] m, int[] h)
{
if (m.length != h.length) // ERROR CONDITION
return -1;

Arrays.sort(mice);
Arrays.sort(holes);

int n = m.length;

int max = 0;
for (int i=0; i< Math.abs(m.get(i) - h.get(i)))
max = Math.abs(m.get(i) - h.get(i));

return Math.abs(max);
}

Time Complexities:

This code will take O(n) time if the arrays are sorted in ascending order. But since we are also sorting the array inside the function, it will take O(n.lg(n)) time.

Greedy Algorithm for Egyptian Fraction

In early Egypt, people used to use only unit fraction (in the form of (1/n)) to represent the decimal numbers.

The fraction was always written in the form 1/n , where the numerator is always 1 and denominator is a positive number. All other fractions were represented as the summation of the unit fractions. For example, 3/4 = 1/2 1/4.

Given a positive fraction, write it in the form of summation of unit fractions.

Example:
2/3 = 1/2 1/6
6/14 = 1/3 1/11 1/231
12/13 = 1/2 1/3 1/12 1/156

Greedy Solution:

For a given number of the form ‘nr/dr’ where dr > nr, first find the greatest possible unit fraction, then call the function recursively for the remaining part.

For example, consider 6/14. First find ceiling of 14/6, i.e., 3. The first unit fraction becomes 1/3.

The remaining fraction is 6/14 – 1/3 = 4/42. Now repeat the same algorithm for 4/42. The ceiling of 42/4 is 11. So the next unit fraction is 1/11.

Now we are left with 4/42 – 1/11 = 1/231. This is a unit fraction itself. So we stop the recursion. We stop when the result is a unit fraction.

6/14 = 1/3 1/11 1/231

class Egyptian Fraction
{
static void printEgyptian(int nr, int dr)
{
if (0 == nr || 0 == dr)
return;

// IF nr IS MULTIPLE OF nr. THEN NOT A FRACTION
if (nr % dr == 0)
{
System.out.print(nr / dr);
return;
}

// IF ALREADY A UNIT FRACTION. OR CAN BE DIRECTLY CONVERTED TO IT.
// i.e dr divisible by nr
if (dr % nr == 0)
{
System.out.print("1/" dr / nr);
return;
}

if (nr > dr)
{
System.out.print(nr / dr " ");
printEgyptian(nr % dr, dr);
return;
}

// PRINT ceiling(dr/nr) AS CURRENT FRACTION
int n = dr/nr 1;
System.out.print("1/" n " ");

// Recur for remaining part
printEgyptian(nr * n - dr, dr * n);
}
}

Note that there exists multiple solution to the same fraction. For example:

3/4 =  1/2   1/4

3/4 =  1/2   1/5  1/20

Greedy Solution to Activity Selection Problem.

Given n activities with their start and finish times. Select the maximum number of activities that can be performed by a single person, assuming that a person can only work on a single activity at a time.

You cannot perform the activity before it starts. The start and end times for each activity are fixed. This is different from the Job selection problem where each activity takes unit time and can be picked at any time before the deadline.

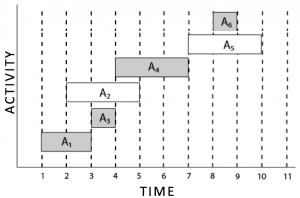
Example 1 : If there are 3 activities as below (StartTime, FinshTime):
{ (2,5), (1, 10), (5, 8) };
The first activity starts at time-2 and finish at time-5.Second Activity start at time-3 and finist at 7 and the 3rd activity start at 5 and finish at 8.

If 2nd activity is picked then the first and third cannot be picked. But 1st and 3rd can be completed by the same person (because they are not overlaping).

Note that we are not trying to optimize the performance, we are just trying to complete maximum number of activities. For example, in the above example, the person will be busy from Time 1 to 10 if he picks up the second activity.

If the following activities are given.

Then we can pick a maximum of 4 activities (A1, A3, A4, A6). Because they are not overlapping with each other.

Solution:

We can use the following Greedy Algorithm to solve this problem:

Sort all the activities in ascending order on their finishing time.
Select the first activity and print it (It will be picked).
Iterate all the activities starting from the 2nd activity and do the following:

If start time of current activity is greater than or equal to the finish time of last picked (selected) activity then pick this activity and print it, else drop the activity and move to the next activity.

Basically, we want to pick a non-conflicting activity that finishes at the earliest, so that it the chances of conflict with the next activity is minimum.

Java Code:

class ActivitySelection
{
class Activity
{
int start;
int end;
String name;
}
public static void printMaxActivities(Activity arr[], int n)
{
// IMPLEMENT THIS FUNCTION TO SORT THE ARRAY ON arr.end.
quickSort(arr);

// SELECT FIRST ACTIVITY
System.out.print(arr[0].name + " ");

int prev = 0; // PREV SELECTED ACTIVITY
for(int cur = 1; cur < n; cur++)
{
if (a[cur].start >= a[prev].end)
{
System.out.print(a[cur].name + " ");
prev = cur;
}
}
}
}

We  need to define the quickSort function that will take an array and sort it on the end field.

Time Complexity:

The function will take O(n) time. But because we are also sorting the array, the sorting will take O(n.lg(n)) time.

The activity selection problem can be used in scheduling multiple competing events in a room, such that each event has its own start and end time. It can also be used in scheduling the manufacturing of multiple products on the same machine, such that each product has its own production timelines.

Job Sequencing with given deadline

Given n Jobs, with their deadline (between 1 to n) and associated profit. Each job takes unit time to complete and you will get the profit only (when the job is completed before the deadline. Sequence the jobs in a way that the profit is maximized.

This problem is one variation of the Activity Selection Problems.

Example1.

Input:
Job: J1, J2, J3, J4
Deadline: 4, 2, 1, 1
Profit: 25, 20, 10, 30

Output: J4, J2, J1 (This is the Sequence of Jobs that will give us max profit).

Example2.

Input:
Job: J1, J2, J3, J4, J5
Deadline: 2, 1, 2, 1, 3
Profit:100, 20, 40, 30, 70

Output: J1, J3, J5 (This is the Sequence of Jobs that will give us max profit = 100+40+70 = 210).
(Note that the sequence can be also. So the order within the sequence is not important as long as the job is finished before the deadline)

Exponential Solution:

Generate all subsets of the given jobs and check individual subset for the feasibility of jobs in that subset (i.e all the jobs in that subset should be do-able before their deadline). Return the maximum profit among all feasible subsets.

The time complexity of this solution is exponential and it is also difficult to implement.

Greedy Solution:

Sort the jobs in decreasing order of their profit. After sorting, the jobs in the second example will look like below:

Job: J1, J5, J3, J4, J2
Deadline: 2, 3, 2, 1, 2
Profit:100, 70, 40, 30, 20

Now iterate over the jobs linearly, and for each job do the following:

Find the maximum timeslot Ti which is empty and is also

Code:

// PROGRAMMING LANGUAGE: C++
void JobScheduling(Job* arr, int n)
{
// Sort the jobs in decreasing order of profit
quickSort(arr); // Need to Implement this function

int result[n]; // FINAL RESULT
bool freeSlot[n]; // TIME SLOTS

// INITIALLY ALL SLOTS ARE FREE
for (int i=0; i=0; j--)
{
if (freeSlot[j])
{
result[j] = i;
freeSlot[j] = false;
break;
}
}
}

// Print the result
for (int i=0; i<< arr[result[i]].id << " ";
}

Time Complexity of this solution is O(n^2). 

Max Distance between two occurrences of the same element

Given an array of integers where elements may be repeating in the array. Find the maximum distance between two occurrences of the same element in the array.

For example:

Input array:
int[] a = {5, 4, 8, 1, 2, 6, 4, 5, 2, 8, 9, 1, 6, 4};
Output: 12

(The distance between first and last occurrences of 4 in the array).

Solution – 1 (Brute Force):

The brute-force solution for this problem is to pick each element in the array and then find the first and last occurrence of that element in the array.

public static int getMaxDistance(int[] arr)
{
int maxDist = 0;
for(int i=0; i maxDist)
maxDist = lastOcc - firstOcc;
}
return maxDist;
}

This solution takes O(n^2) time. The next solution uses an extra memory for Hash but solves the problem in linear time.

Solution -2 (Using Hash)

Use a hashmap. Traverse the given array and store index of the first occurrence in the hash.

For every other occurrence, find the difference of that index from the first index stored in the hash. Keep a track of the maximum distance found till now.

Code:

public class RitambharaUtils
{
public static int getMaxDistance(int[] arr)
{
if(arr.length == 0){ return -1; } // WHEN ARRAY HAS 0 ELEMENTS

HashMap hash = new HashMap();

int maxDistance = 0;

for (int i = 0; i < arr.length; i++)
{
if (!hash.containsKey(arr[i]))
{
hash.put(arr[i], i);
}
else
{
int dist = i - hash.get(arr[i]);
if(dist > maxDistance)
maxDistance = dist;
}
}
return maxDistance;
}

public static void main(String[] args)
{
int[] a = {5, 4, 8, 1, 2, 6, 4, 5, 2, 8, 9, 1, 6, 4};
System.out.println(getMaxDistance(a));
}
}

Swapping two variables without using third variable

This is a very common interview question, esp. at the junior level. Let us first write a function that swap two integers using a third variable.

void swap(int *a, int *b){
int temp = *a;
*a = *b;
*b = temp;
}

It must receive int* and not int, because we want to change the variables in calling function. In C++ variables can be passed by reference also,

// C++ Code. Won’t compile for C language.
void swap(int &a, int &b)
{
int temp = a; a = b; b = temp;
}

But C language does not permit pass-by-reference. It is easier to answer when the question is about swapping two integers. The question here is to swap two variables. A variable can be of any data type, either pre-defined or user-defined.

Before getting into these details, let us try to dissect popular answers,

Method-1: Using XOR Method

Using bit-wise XOR operator, two integral variables can be swapped without using third variable as shown below:

X = X ^ Y;
Y = X ^ Y;
X = X ^ Y;

But XOR operator can only be used with integral data types. We cannot use this method to swap two floating point numbers of either single precession or double precession. Let us look at the next method:

Method-2: Add-subtract method

The second method is using a combination of addition and subtraction operators, as shown below

X = X + Y;
Y = X - Y;
X = X - Y;

This method can swap two numbers of any type, but it is worse than previous method. If values of x and y are so large that their sum exceeds upper limit of their data type, then overflow happens. How C language handles overflow and underflow is not defined.

You may replace combination of add-subtract with multiply-divide, but problem of overflow is still there.

One limitation with both the methods is that they can only be used with predefined data types. They cannot swap two strings or even two pointers. In fact, even a code similar to Code 3.5 fails to swap two string. To swap two strings, we have to write a custom swap method as given in Code below:

// str1 AND str2 ARE OF EQUAL LENGTH
void swap(char* str1, char* str2)
{
int len = strlen(str1);
for(int i=0; i

Similarly, to swap two arrays or two objects of user-defined struct type, we have to write custom methods. While swapping user defined types, the complications of shallow-copy and deep-copy may also arise. There is no generic swap method that can swap two variables.

Now, you know what to answer, when interviewer asks you to swap two variables without using third variable. With your answer, you may end up educating the interviewer.

Count max points on a line

Given n points on a 2D plane with (x, y) co-ordinates. Find the maximum number of points lie on the same straight line. For Example, If given points are: { (1, 1), (2, 2), (2, 1), (4, 3), (3, 3), (1, 4) }
Then the output should be 3 because there are 3 points on the same line: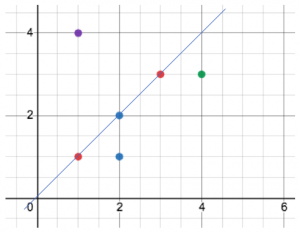

Solution:

We can draw a line between each pair of points. The brute force way of solving this problem is to check how many points fall on every such line.

If you know two points falling on the line, then you can find the equation of the line, which is in the following form:

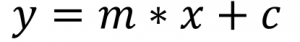
In this equation, m is the slope. If you are given two points (x1, y1) and (x2, y2), then the slope is: m = (y2-y1)/(x2-x1) 

The slope remains the same for a line. Follow the below algorithm:

For each given point, find the slope of that point with all other points. If the slope of this point with two other points is same, then these three points (the 2 points and the point of origin) are considered to be in the same line.

We do it for all the points, and keep a track of the maximum points on one line seen till now.

Maintain a HashMap for each point. The slope between two points become the key and value is the frequency (number of points) with that slope. The problem here is that slope is a double value and we may run into precision errors. So to avoid this, store the slope as a rational number instead of double. To get the same number for 5/10 and 7/14, store the GCD (i.e 1/2).

class Point {
int i;
int j;
Point() { i = 0; j = 0; }
Point(int a, int b) { i = a; j = b; }
}

public class Test
{
public static int maxPointsOnALine(Point[] points)
{
int result = 0;
HashMap> map = new HashMap<>();

for (int i = 0; i < points.length; i )
{
map.clear(); // USING FRESH MAP FOR EACH POINT

int overlap = 0;
int max = 0;

for (int j = i 1; j < points.length; j )
{
int x = points[j].i - points[i].i;
int y = points[j].j - points[i].j;

// IF TWO POINTS ARE SAME
if (x == 0 && y == 0) {
overlap ;
continue;
}

int gcd = generateGCD(x, y); // FIND GCD

if (gcd != 0) // BRING x AND y TO SIMPLEST FORM
{
x /= gcd;
y /= gcd;
}

if(map.containsKey(x))
{
if(map.get(x).containsKey(y)) // OLD POINT
map.get(x).put(y, map.get(x).get(y) 1);
else // NEW POINT
map.get(x).put(y, 1);
}
else
{
HashMap m = new HashMap<>();
m.put(y, 1);
map.put(x, m);
}
max = Math.max(max, map.get(x).get(y));
}
result = Math.max(result, max overlap 1);
}
return result;
}

private static int generateGCD(int a, int b)
{
if (b == 0) return a;
return generateGCD(b, a % b);
}
public static void main(String[] args)
{
Point[] points = new Point[]{
new Point(1, 1),
new Point(2, 2),
new Point(2, 1),
new Point(4, 3),
new Point(3, 3),
new Point(1, 4)
};
System.out.println(maxPointsOnALine(points));
}
}

Print all Subsequences of an Array

Given an array of integers, Print all possible subsequences of that array.

A subsequence is a sequence that can be derived from another sequence by deleting some or no elements without changing the order of the remaining elements. (Definition from Wikipedia).

If the input array is { 1, 2, 3, 4, 5, 6, 7, 8}, then following are the subsequences:

{1, 3, 5}
{1, 8}
{1, 2, 3}
{}
{1, 2, 3, 4, 5, ,6 7, 8}

But following are not subsequences:

{1, 5, 3} // The Order of elements is not same as Original array
{1, 9} // 9 is not part of original array

Solution:

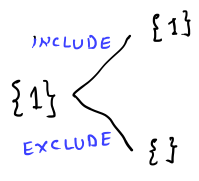
The order of elements in the main array and subsequence remains the same, so essentially, at each element, we have two choices, either to include the element or exclude it. By following these choices at each element, we can generate all the subsequences.

If the input array is {1} (with only one element). Then two possible subsequences are:

If the array is {1, 2}, then we have to make the decision (Include / Exclude) for both the elements.

Similarly, we can extend the solution for n elements.

Java Code:

public class Temp {
public static void printArray(int[] a, int n)
{
System.out.println();
for(int i=0; i= arr.length)
{
printArray(ss, j); // PRINT FIRST j ELEMENTS OF ss
return;
}

// INCLUDING THE CURRENT ELEMENT OF arr
ss[j] = arr[i];
printAllSubSequences(arr, i+1, ss, j+1);

// EXCLUDING THE CURRENT ELEMENT OF arr
printAllSubSequences(arr, i+1, ss, j);
}

public static void main(String[] args)
{
int[] a = {1, 2, 3, 4};

// TEMP ARRAY TO HOLD SubSequence.
// This can go in the wrapper function
int[] ss = new int[4];
printAllSubSequences(a, 0, ss, 0);
}
}