The Sword and Laser discussion
Time Dilation -- How's that work?
date
newest »
newest »
I hope this is the right video (I can't watch it at work. Too much commotion). Hawking talks about time dilation in his series Into the Universe. He explained it pretty well for me and helped me understand the concept. Hope it helps!http://www.youtube.com/watch?v=02tchl...
To answer the "also" part, Star Trek never seriously addresses time dilation effects. Warp Drive (and Hyperspace in other similar settings) allow vehicles to move outside our universe's frame of reference, so they're effectively side-stepping the issue. (In reality, if this were possible it would lead to a number of problematic paradoxical effects, up to and including arriving at your destination before you left).However, I believe I did read somewhere that part of the idea behind Trek's Star Dates is that the Star Date system is designed to allow easy compensation for time-dilation-related date discrepancies between distant ships and stations.
Ah, getting to re-post previous answers is glorious! This thread from the group's Hyperion discussion may also be elucidating.Here are the basics for relativistic travel (travel near the speed of light).
Imagine a clock that is composed of 2 mirrors (A and B) facing each other with a separation of length L. A single photon of light is bouncing between them, and each time the photon hits A, the clock ticks once.
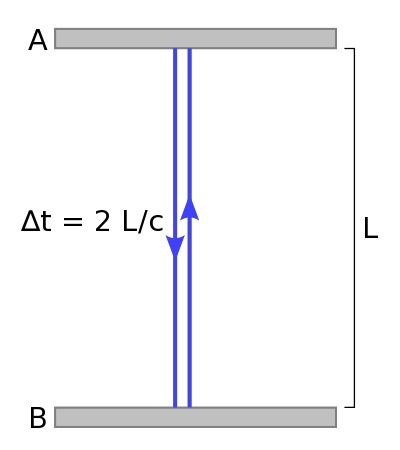
Then we know that the time between ticks is
(where c is the speed of light, a constant). With me so far?Now imagine that you're moving parallel to this clock at speed v, such that you are seeing the light trace a different path, as so:
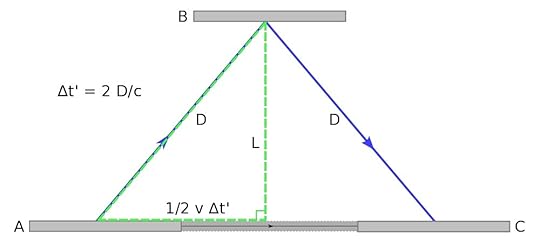
Now, and this is important, from your perspective (i.e. frame of reference), the light is traveling a distance 2D rather than 2L, making the period of the clock
See the right triangle? The Pythagorean Theorem (
) tells us that 
.Do a little math (substitute D into the 2nd equation and solve for delta t'), and you reach the following:
But look! That part on top is just our earlier equation for the observed time when you're at rest, therefore:
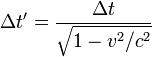.What does this mean? As v approaches c, the denominator of the equation approaches zero, which means that the observed time of a person moving in a very very fast frame of reference will grow very very large the closer they come to the speed of light.
I doubt anyone's actually read this far, but I swiped all the images from http://en.wikipedia.org/wiki/Time_dil..., where you can go for a more thorough explanation.
I think that's pretty hard to explain without some serious math. It's a bit like asking why gravity attracts objects. Speaking of which, a current theory suggests that dark matter will accelerate time.. weird stuff :)
AndrewP wrote: "Speaking of which, a current theory suggests that dark matter will accelerate time.. weird stuff :) "Swifter and more seductive is the dark side.
If only you knew the power of the dark side!I was about to say the same as AndrewP. "Why does it happen?" without math is actually a philosophical question like "why is there a cosmos" or "what's the meaning of life".
We are used to take time for granted in our (newtonian) everyday life. All the other things change in relation to time but we consider time to flow its way unconcerned of what's going on. But in reality this doesn't happen. It's just that we are used to low speed and low energies. If we speed things up we see that newtonian laws aren't precise anymore and relativity is more accurate.In fact,relativity laws are fine for everyday life too; we just prefer the simplicity of the newtonian ones(for low speeds they're the same).
Without fancy calculus now,think of that: In accerelated movement speed is related to time,right?
V=Vo+a*t (V-speed,Vo-initial speed,a-acceleration,t-time).
So obviously time is related to speed too,
t=(V-Vo)/a.
In highscool newtonian physics we usually deal with uniform acceleration so a is a nice solid,steady number. But in relativity we always have this square root of 1 minus V squared/C squared (C is 299,792,458 metres per second,the speed of light) which causes time to change differently(time dilation).
We normally experience time in a linear 2d reference but when we go really fast we jiggle around the 3d wibbley wobbly timey-wimey dimensions. I learned everything I know about astrophysics from Dr Who so that's legit.
Phillip wrote: "So a person moving really fast (like approaching the speed of light fast) leaves earth on a round trip that to him subjectively takes 2 years;"I haven't really seen this explained properly. I believe what you described is commonly known as the Twin Paradox. Where one twin is on earth while another does the round trip and returns having aged younger. The problem I have understanding is, if the twin doing the round trip is moving away from earth say - both twins are still moving just as fast away from each other relative to each other. The answer, from what I can gather, has to do with acceleration - one twin is accelerating and this makes a difference. But that still does not take into account that the speed factor is still then totally irrelevant.
Then what happens if we use triplets instead of twins. Two triplets take an equivalent round trip at equal velocity and acceleration but in opposite directions to the stationary triplet. Now when the travelers return they should both be younger than the stay at home triplet - but what difference in age should the travelers be to each other? Because each travelling triplet should have been ageing slower again compared to each other than each is to the stationery triplet.
Now my head hurts.
David Sven wrote: "Some stuff about twins... maybe triplets?"The equations are pretty straightforward, and direction doesn't matter. Here, take a look:
The Story of A and B
Suppose there is a pair of twins off on some planet. Their parents pragmatically decided to name them A and B, to avoid confusion.
Well, one day, a space traveler visits the planet. He's so impressed with the twins' names, that he offers them a (randomly chosen) 10√3 Year ride on his wonderful spacecraft.
Twin A jumps at the opportunity, having always harbored a secret passion for adventure that just wasn't being met on their little planet. Twin B, however, is afraid of flying... also space, time, and rather large rabbits, and so politely declines and goes back to making clogs (their planet's principle export).
Twin A swears to tell B all about the trip. Twin B promises to do nothing but make clogs until A returns.
Fortunately for me, the space traveler has a truly marvelous ship, capable of accelerating to a significant fraction of the speed of the light, let's say... 50%, or 0.5c, instantaneously, thereby eliminating pesky things like time spent accelerating from my equation (although, I guess I could just say that it moves at an average of 0.5c for the duration of the trip... six of one, half-dozen of the other).
So we have...
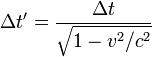
v = 0.5c, so v^2 = 0.25c^2, so the denominator becomes 0.5√3. This means that for every year on board the ship, 2/√3 years pass on the planet.
Which naturally leads to A arriving home and rushing to tell B that there were no rather large rabbits at all... only to find that their house and village have been flooded with clogs.
A asks B, "How on (name of planet) did you make so many clogs in only 10√3 years?"
B answers, "10√3? A... you were gone exactly 20 years. Where have you been all this time? Yikes, time!"
A looks up at the stars wistfully. "Ah, B... I only wish I had a firm grasp of relativistic physics so that I could explain it to you."
fin
Ha ha! Thanks for that Sky. Nice analogy. My problem isn't really with understanding your math. I did strain my brain really hard when I saw you first post this on the Hyperion thread and I got it - My question would be that even though twin B doesn't go anywhere, he is still also moving at V relative to twin A. So how does the equation favor A to experience time dilation over B? Light as far as I know doesn't actually know or care which twin is moving. Or am I looking at it all wrong?
David's got an interesting point, at least from the point of view of someone who knows just enough physics to be dangerous, but who hasn't studied it extensively.As I understand it, there's no such thing as absolute, objective velocity, since that posits some over-arching frame of reference (henceforth, FoR) that contains and controls everything. Since we know that that doesn't exist, the best we can do is measure velocity relative to a convenient FoR which is appropriate to the things being measured. For stuff here on earth, we tend to pick the earth itself--my car is moving 65 MPH relative to the ground. But back out a bit further, and that FoR ceases to be useful (or, rather, it gets confusing--from the earth-centric FoR, the sun apparently orbits the earth, but the other planet's paths are very, very complicated; switching to the sun-centric FoR, however, allows us to see the mathematically elegant elliptical patterns; but that also means that my car is moving about 67,000 MPH even when parked!).
Most of the time-dilation thought experiments I've seen use a planetary FoR. Sky's example above has A zipping around at relativistic speeds from B's "stationary" point of view...but isn't the FoR used in the experiment relative? Wouldn't it be just as accurate to say that, from A's point of view, B is the one moving quickly? Or does it have to do with the mass of the objects surrounding A and B (since B is on a planet, that's my best guess what's happening)--what if A is on a Super Star Destroyer, and B is on an X-Wing, and one or the other moves at relativistic speeds to the other...what happens then? Whose time gets dilated?
Gah, my head hurts now. :(
Oh, I got you. Okay, there are a couple of ways of looking at this. You could consider that there are actually 3 inertial frames of reference at work (because the twin on the ship will change directions, creating a non-inertial frame of reference between the 2 inertial frames).Instead, let's talk Lorentz contraction: the decrease in length between objects detected by an observer moving at a non-zero velocity relative to the objects, inversely proportional to the Lorentz factor:
where 
From my example, we could easily say that twin A was going a distance of 5 light years (for a round trip of 10 light years). We already know that the velocity is v = 0.5c
Twin B, retroactively enlightened after making the perfect clog, decides to calculate the time it will take A to make the trip. Well, that time will just be T = D/v = (10 years)c/(0.5c) = 20 years. Having also grasped the fundamentals of special relativity, B calculates that A will actually experience 10√3 years of time, as shown above.
Twin A will also perform the calculation, but because of Lorentz contraction, from A's frame of reference the distance between the planet at the destination is observed to be the actual distance divided by the Lorentz factor, or (10 years)c(√3/2) = 5√3 light years. So A observes traveling less than the actual distance. Then, from A's perspective, the time taken will be T = D/V = 5√3c/0.5c = 10√3 years.
Does that clarify anything for you?
Sky wrote: "Does that clarify anything for you? "Perfectly :( - It gives me something interesting to do my head in for a bit though. Thank you. I'm still not sure yet that it touches the objection raised. I understand that there are 3 different time references - but I'm still not certain that answers why A is considered to be moving relative to B wile B is considered stationery relative to A.
I think you are confusing the motion of A relative to B and the motion of A or B relative to space itself. I think, only the second one really counts.To make your head hurt even more, if A and B are both traveling close to the speed of light towards each other, what is their relative velocity? Normal math would say it's c x 2, but we know it cannot exceed c. (That's my simplest example of how normal math fails at relativistic speeds.)
AndrewP wrote: "I think you are confusing the motion of A relative to B and the motion of A or B relative to space itself. Only the second one really counts."Um...relative to space itself? Does that mean that there is some over-arching frame of reference after all? I thought one of the first principals of relativity was that there isn't a "universal" frame of reference.
o_O
OK, I'll take a stab at explaining this without maths. Space and time are one indistinguishable unit. You cannot define the one without the other.Time dilation occurs everywhere. Your feet don't age as quickly as your head (approximately 90 billionths of a second over a 79-year lifetime). Our GPS need to be recalibrated approximately 7 times a minute, or they'd be tens of kilometres/miles off. Time dilation due to flying across the Atlantic and back has been physically measured using atomic clocks.
Using the Twin Paradox, B sees A as slowing down, as if working in molasses. Conversely, A sees B as running around whipping out clogs. It doesn't matter if B is moving away or towards A, only that B is travelling relatively faster. Both are experiencing their own level of time dilation, but it's for simplicity sake we pretend A is stationary and not having time ellipsed.
As for Star Trek, Warp Speed is a method of bending the 'fabric' of spacetime, like experienced in a gravity well. As time in that bubble occurs faster than outside, they can appear to travel faster than light. This in theory negates the time dilation, by changing the distance between two points.
AndrewP wrote: "Normal math would say it's c x 2, but we know it cannot exceed c. (That's my simplest example of how normal math fails at relativistic speeds.)"Except "Normal" math doesn't fail. Even relativity is underpinned by normal math.
Relativity puts a cap on c. Does that mean that there is an actual real cap on C? Or does it only really proves that Relativity has a limit of application for FTL speeds?
It's fun for example when Doctor Who runs up against paradoxes in time. Of course paradoxes don't actually have a physical interpretation - thats why they are paradoxes. Rather they show us the limits of application of relativity - I think.
Okay. So, yeah, good stuff. After reading everyone's responses, I think, what I've come away with is the following:Time is not a huge encompassing entity or thing through which we move. Time is actually unique to each individual, and is relative to the individual's position in the universe and the speed at which the individual is moving. So, for me, time is different than it is for my brother, however, because we're both living on Earth and moving through the universe at relatively similar speeds (the fastest I ever go is when I'm on an airplane) the difference in our experienced times is negligible at best. For practical intents and purposes, time for everyone on Earth is more or less the same (even though it's just the tiniest bit different)... because we're on Earth. The speed at which Earth moves through the universe (and it's gravitational force acting upon us) more or less supersedes the speeds which we move while we're on Earth.
This kind of makes sense. Time is unique to me. So if I'm not on Earth, if I'm moving at a different speed, time is going to be different as well. So, time dilation affects everyone. Time dilation is your unique time. It is your experienced time relative to your position and speed in the universe, and since two people can't occupy the same space in the universe... time is different for everyone. That's what time dilation is. The affects become more apparent when the difference in speed and gravity is greater between two individuals.
I know, I'm fairly sure I repeated myself there, several times actually. Also, totally changed tenses multiple times. It helped me, though, to write it through.
Even if I'm not understanding this correctly, let's all just play along, and pretend I get it. Or at least that I get a tiny bit of it. My stomach doesn't hurt anymore and that's what's important.
Now, I'm gonna go read a bunch of Flash comics. There's gotta be a bunch where he just like vibrates himself into the future.
"But that still does not take into account that the speed factor is still then totally irrelevant. "You're talking about a spaceship that accelerates and leaves Earth,then again to stop and accelerate towards Earth and stop again reaching Earth. Speed obviously changes,the astronaut accelerates.
"So how does the equation favor A to experience time dilation over B?"
The astronaut's frame of reference isn't inertial due to this thus we have the "paradox".All intertial frames of reference are equivalent to the laws of physics so yeah,if A's FoR was inertial he should expect the same as B but it isn't.
"Time is not a huge encompassing entity or thing through which we move. Time is actually unique to each individual, and is relative to the individual's position in the universe and the speed at which the individual is moving"
That's pretty much the difference between classic newtonian physics(considering time and space universal and the same for everyone)and relativity(which says time and space are not universal but ehm...relative).
This is a subject that comes up quite a bit in Science Fiction, and that's a good thing because well, it's real. However, whenever I think about it too much it actually makes my stomach hurt. It's a hard concept to really wrap my brain around. Let me explain what I think I understand, then maybe you can help me actually understand. Don't worry, I read the wikipedia article.
Time Dilation occurs when something (or usually in SF someone) moves really fast, or is far away from Gravity, or both. To quote the wiki "velocity and gravity each slow down time as they increase."
So a person moving really fast (like approaching the speed of light fast) leaves earth on a round trip that to him subjectively takes 2 years; however, all the people who aren't moving at the same speed as the really fast moving person (say all the normal people on earth) to them time moves on and they experience decades passing before the guy who went to space returns. So for person A the trip took 2 years, to the rest of us his trip took 20 years.
That's my broad strokes, without specifics understanding of Time Dilation.
I guess what bothers me is, why does this happen? Why does speed affect the flow of time, why does an object when acted upon by gravity affect time? It's hard to understand why time can be affected by these forces at all.
So what am I missing? Can you explain why this happens without using too much higher order math? What I mean is, I never took Calculus. Maybe math is the only way to explain the why, though. In that case, I'm screwed.
Also:
For people who are Star Trek fans, why doesn't Time Dilation affect those on the Enterprise? Or does it? In the original series they talk about going on a 5 year mission, but they're going really fast. On earth who knows how much time would pass... more than 5 years though. This doesn't seem to be the case, however. It seems 5 years whether you're on a starship or 5 years on earth are the same.
So, anyway, thoughts? Anyone?
-Phillip