For some hard to explain reason, I really got a kick out of this post at the blog Math With Bad Drawings, which I’m sure you all check in with frequently, as I do.
Anyway:
What is the biggest problem facing humanity this week?
A. The threat of Grexit*
B. The bittersweet knowledge that someday, when all of this has passed, we’ll have fewer opportunities to use the amazing word “Grexit”*
C. People thinking functions are linear when they’re SO NOT LINEAR
D. Other (e.g., cat bites)
You see? Share this with your colleagues and I expect hilarity to ensue.
If you answered C, then congratulations! You are probably a teacher of math students ages 13 to 20, and we all share in your pain.
For everyone else (including you poor cat-bitten D folk), what are we talking about? We’re talking about errors like these (warning—mathematical profanity ahead):
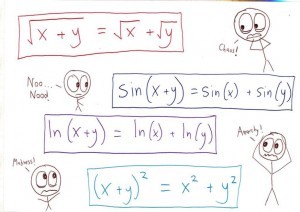
C
NOW the hilarity, right?
Okay, okay, if you don’t teach students algebra ever, then maybe this post won’t strike you as funny, sad, and so very very true.
I don’t blame the kids, of course. These errors are a natural—perhaps even inevitable—byproduct of the way we teach mathematics.
It sure is. Not quite inevitable, I hope, but if we could somehow bottle Ben Orlin (the author of the site) and have him teach ALL the math, then, well, a) everyone would find the above errors funny rather than funny + sad + depressing or else incomprehensible, and b) everyone would coast through algebra, and c) I would never again have to demonstrate to a student that indeed, you cannot distribute an exponent through parentheses, not simply because it is against the rules, but because it does not work.
Also, if by chance you do teach math, this blog is a good one to check in on from time to time. Ben is quite good at conceptualizing errors and seeing why the error is made and how to explain properly why it’s wrong.
The distributive law is crucial. It underlies most of what we do in algebra, such as factoring and “gathering like terms.” So what’s the problem?
It’s that students don’t learn the distributive law as a fact about numbers. They learn it as a fact about parentheses.
And unfortunately, mathematicians use parentheses in two very different ways: first, to group numbers; and second, to designate the inputs of a function.
I knew that. But Ben explains it better.
* I had to google the term.

 newest »
newest »
 newest »
newest »
 Most of my students are much older, but have been out of school so long they don't remember any math to speak of. Although often the older students at least know some arithmetic, which often the younger students who just graduated from HS really do not.
Most of my students are much older, but have been out of school so long they don't remember any math to speak of. Although often the older students at least know some arithmetic, which often the younger students who just graduated from HS really do not.
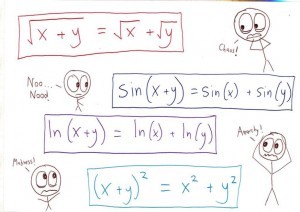




I usually start my first tutoring session by asking them (at any age) why a negative times a negative is a positive and use that answer to determine how to approach teaching them. I have always had to follow up with a physical visualization of the concept.