Lance Fortnow's Blog, page 119
September 9, 2013
T/F - No Explanation needed VS T/F-Explanation needed.
One of the comments on my blog on Types of question for exams
A True/False math question where they have to prove their answer. A student who picks the wrong answer can figure that out during the proof and then correct their answer. A student who picks the wrong answer and proves it has proven they really don't have a clue
Actually I once did an experiment about this! It's only one so I don't know what to read into it, but I will describe it and speculate.
CMSC 250 is the Sophomore Discrete Math course, required for all majors. CS 3 is a co-req. It's a course on how to prove simple things. We DO go over how a FOR ALL statement can be true vacuously (E.g.,all of the students over 10 feet tall will get an A+). Around 150 students take the course. In the spring there is an honors section of about 20. I PLANNED the following:
In Spring of 2008 one of the questions on the final was a set of FIVE statements where the students had to, for each statement, say if its TRUE or FALSE and NO JUSTIFICATION NECC. One of the statements was If A is a set of natural numbers such that the powerset of A has 5 elements then A is infinite.
In Spring of 2010 one of the questions on the final was a set of FIVE statement where the students had to, for each statement, say if it's TRUE or FALSE and IF TRUE THEN GIVE A SHORT JUSTIFICATION, IF FALSE THEN GIVE A COUNTEREXAMPLE.
Note that the statement is TRUE since there are NO such sets A.
So, how did they do?
When NOT needing to justify or give a counterexample, of the 150 students in the class, 14 got it right. There was no correlation (or perhaps a very weak one) between those who got it right and those who did well in the course or those that were in the honors section.
When the DID need to justify or give counterexample, of the 152 students in the class, 19 got it right. Slightly stronger correlation to those who got it right and those who did well in the course and to those in the honors section.
I would say the 5 extra students and the slightly better correlation is too small to care about. I was surprised--- I thought being forced to find a countexample would help them along. But this is a rather
tricky question which some non-theory faculty members had trouble with when I explained this story to them. Exam Pressure was likely NOT a factor as my exams have very little time pressure- by the end of the exam
there were only about 30 students left taking it.
Here are the answers I got:
FALSE- clearly A is finite.
FALSE- too obvious to say why.
FALSE- there is no such A
Variants of the above.
Incoherent things that may be similar to the above.
UPSHOTS: This is a failed experiment in that I didn't prove or disprove the hypothesis that asking students to justify makes more students get it. Of course, even if I had shown that it would only be for this one problem. I DID show that this problem is trickier than I thought. I may try this again with a less tricky problem.
Published on September 09, 2013 17:26
September 6, 2013
Myhill Nerode versus Pumping Lemma
I have seen some recent backlash against the pumping lemma for showing that languages are not regular and as I am now teaching regular languages I had to choose should I teach the pumping lemma or Myhill-Nerode to show languages are not regular. Let's review both definitions (taken from Wikipedia)
Pumping Lemma: If a language L is regular, then there exists a number p ≥ 1 (the pumping length) such that every string uwv in L with |w| ≥ p can be written in the form uwv = uxyzv with strings x, y and z such that |xy| ≤ p, |y| ≥ 1 and uxyizv is in L for every integer i ≥ 0.
Myhill-Nerode: Given a language L, and a pair of strings x and y, define a distinguishing extension to be a string z such that exactly one of the two strings xz and yz belongs to L. Define a relation RL on strings by the rule that x RL y if there is no distinguishing extension for x and y. It is easy to show that RL is an equivalence relation on strings, and thus it divides the set of all finite strings into equivalence classes.
The Myhill–Nerode theorem states that L is regular if and only if RL has a finite number of equivalence classes, and moreover that the number of states in the smallest deterministic finite automaton (DFA) recognizing L is equal to the number of equivalence classes in RL. In particular, this implies that there is a unique minimal DFA with minimum number of states.
The two basic complaints about the pumping lemma: Five quantifiers and it is not complete--there are nonregular languages that can be pumped. To the first point if you think of the pumping lemma as a game with the adversary choosing p, x, y and z, the quantification is not as confusing as some would think. Myhill-Nerode also has five quantifiers when you spell it out: For all regular L, there exist x1,...,xk such that for all y there is an i such that for all z, xiz is in L iff yz is in L.
As to the second part, the counterexamples are contrived and usually go away with simple closure properties. Consider the one from wikipedia:
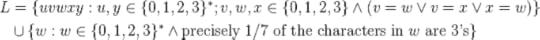
Take L ∩ (01(2∪3))* eliminates the strings in the first part of L and now it is easy to pump.
So I don't buy the arguments for Myhill-Nerode over pumping. Nevertheless I'll teach the pumping lemma and Myhill-Nerode because they are both so cool.
Pumping Lemma: If a language L is regular, then there exists a number p ≥ 1 (the pumping length) such that every string uwv in L with |w| ≥ p can be written in the form uwv = uxyzv with strings x, y and z such that |xy| ≤ p, |y| ≥ 1 and uxyizv is in L for every integer i ≥ 0.
Myhill-Nerode: Given a language L, and a pair of strings x and y, define a distinguishing extension to be a string z such that exactly one of the two strings xz and yz belongs to L. Define a relation RL on strings by the rule that x RL y if there is no distinguishing extension for x and y. It is easy to show that RL is an equivalence relation on strings, and thus it divides the set of all finite strings into equivalence classes.
The Myhill–Nerode theorem states that L is regular if and only if RL has a finite number of equivalence classes, and moreover that the number of states in the smallest deterministic finite automaton (DFA) recognizing L is equal to the number of equivalence classes in RL. In particular, this implies that there is a unique minimal DFA with minimum number of states.
The two basic complaints about the pumping lemma: Five quantifiers and it is not complete--there are nonregular languages that can be pumped. To the first point if you think of the pumping lemma as a game with the adversary choosing p, x, y and z, the quantification is not as confusing as some would think. Myhill-Nerode also has five quantifiers when you spell it out: For all regular L, there exist x1,...,xk such that for all y there is an i such that for all z, xiz is in L iff yz is in L.
As to the second part, the counterexamples are contrived and usually go away with simple closure properties. Consider the one from wikipedia:
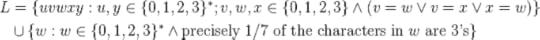
Take L ∩ (01(2∪3))* eliminates the strings in the first part of L and now it is easy to pump.
So I don't buy the arguments for Myhill-Nerode over pumping. Nevertheless I'll teach the pumping lemma and Myhill-Nerode because they are both so cool.
Published on September 06, 2013 07:03
September 3, 2013
Types of questions for exams
QUESTION: Give as many types of exam questions you can, give examples, and comment on if this is a good type of question.
My answer below.
A problem that some students can get right even if they never had the course because they have seen it in some other course. EXAMPLE: In a course on Ramsey Theory have a question that uses the Prob. Method. PRO: The question is still in scope for the courses. CON: A bit awkward that someone may have learned the material elsewhere. UPSHOT: This is FINE.
A problem that some students can get right even if they never had the course because they are quite clever. EXAMPLE: Easy Combinatorics or Probability in a sophomore Discrete Math Course. PRO: The question is still in scope for the courses. CON: A bit awkward that someone may have missed class but still got it right. UPSHOT: This is FINE.
A rigged question--- students saw two examples in class, two examples on the HW and now have to do one themselves. EXAMPLE: proving numbers irrational. PRO: Clearly in scope and fair. PRO: They will surely understand what you are asking for. CON: They may get it right via memory rather than understanding (they may not even know the difference.) UPSHOT: This is FINE though it requires some planning ahead of time.
A rigged question with a twist--- students saw two examples in class, two examples on the HW and now have to do one themselves but its DIFFERENT in an important way. EXAMPLE: In class and HW do many problems like Here is the distribution, here is a random var, what is its expected value but on the exam give Here is a random var, here is what we want for the expected value, give a distribution that gives us that. PRO: Harder to memorize template. CON: May be hard to grade as they say odd things. CON: May be confusing to know what you are asking for, even for good students. UPSHOT: This is FINE though it requires some planning ahead of time.
A problem that requires utter mastery of the material but no creative thought. EXAMPLE: Give the algorithm (that we did in class) for proving that a CFG's are in P. Write it up so that someone who had never seen it can understand it. PRO: Straightforward yet hard to get via memorization. CON: Might be too time consuming for an exam. CON: (From experience) no matter how much you say in bold letters things like Write it up so that someone who had never seen it can understand it. They will skip steps and write it up badly and its hard to tell if THEY really know it. UPSHOT: I do this but only in certain cases.
A problem that requires them to be creative (this is ill defined but its the opposite of the one above). PRO: If they truly understand the material they can do this. CON: My PRO may be incorrect. UPSHOT: Absolutely fine for HW which are not worth much for the grade anyway and I can enlighten them. I tend to avoid these on exams. Though the line between creativity and standard is a thin one. (Problem for an exam: How thin in millimeters?)
A giveaway question. When I teach Formal Lang Theory I have (going back to when I was Harry Lewis's TA in 1981) have on the exam Give an example of a string of length 4 over the alphabet {a,b}. An unintended consequence- if they CAN"T do this its a really bad sign. I have asked this question many times and I have literally NEVER seen someone get it wrong and pass the course. I have gotten the following answers: ab*, ababa, and a DFA recognizing aaaa (that I was tempted to give credit to but did not). Incidentally, the most common right answer has always been abab. Second is abba. PRO: I have this one early in the exam to calm them down.
I try to ask some of each type on an exam. However, sometimes a question can be easier or harder than you intended, or be harder to grade then you thought, or not be in category you thought it would be in. The hardest line to draw is which questions are a matter of mastery and which are a matter of creativity? Another issue- some students can abstract better than others.
When teaching a large course such as Sophomore discrete math (150-200 students) I tend to get a uniform distribution skewed a bit on the high side. More precise: I tend to get at roughly 10 students in EVERY 10-point interval: 0-10, 10-20, 20-30,..., 90-100, with less on the low side and more on the high side. The benefit of this is that the students who get (say) less than 40 CANNOT say Well--- everyone did badly. They really are send a signal to either work harder or drop (I tell them this directly as well). I don't understand profs who give exams where nobody cracks 50/100 (I have heard this is common in Physics). They are wasting half of the grade spectrum.
My answer below.
A problem that some students can get right even if they never had the course because they have seen it in some other course. EXAMPLE: In a course on Ramsey Theory have a question that uses the Prob. Method. PRO: The question is still in scope for the courses. CON: A bit awkward that someone may have learned the material elsewhere. UPSHOT: This is FINE.
A problem that some students can get right even if they never had the course because they are quite clever. EXAMPLE: Easy Combinatorics or Probability in a sophomore Discrete Math Course. PRO: The question is still in scope for the courses. CON: A bit awkward that someone may have missed class but still got it right. UPSHOT: This is FINE.
A rigged question--- students saw two examples in class, two examples on the HW and now have to do one themselves. EXAMPLE: proving numbers irrational. PRO: Clearly in scope and fair. PRO: They will surely understand what you are asking for. CON: They may get it right via memory rather than understanding (they may not even know the difference.) UPSHOT: This is FINE though it requires some planning ahead of time.
A rigged question with a twist--- students saw two examples in class, two examples on the HW and now have to do one themselves but its DIFFERENT in an important way. EXAMPLE: In class and HW do many problems like Here is the distribution, here is a random var, what is its expected value but on the exam give Here is a random var, here is what we want for the expected value, give a distribution that gives us that. PRO: Harder to memorize template. CON: May be hard to grade as they say odd things. CON: May be confusing to know what you are asking for, even for good students. UPSHOT: This is FINE though it requires some planning ahead of time.
A problem that requires utter mastery of the material but no creative thought. EXAMPLE: Give the algorithm (that we did in class) for proving that a CFG's are in P. Write it up so that someone who had never seen it can understand it. PRO: Straightforward yet hard to get via memorization. CON: Might be too time consuming for an exam. CON: (From experience) no matter how much you say in bold letters things like Write it up so that someone who had never seen it can understand it. They will skip steps and write it up badly and its hard to tell if THEY really know it. UPSHOT: I do this but only in certain cases.
A problem that requires them to be creative (this is ill defined but its the opposite of the one above). PRO: If they truly understand the material they can do this. CON: My PRO may be incorrect. UPSHOT: Absolutely fine for HW which are not worth much for the grade anyway and I can enlighten them. I tend to avoid these on exams. Though the line between creativity and standard is a thin one. (Problem for an exam: How thin in millimeters?)
A giveaway question. When I teach Formal Lang Theory I have (going back to when I was Harry Lewis's TA in 1981) have on the exam Give an example of a string of length 4 over the alphabet {a,b}. An unintended consequence- if they CAN"T do this its a really bad sign. I have asked this question many times and I have literally NEVER seen someone get it wrong and pass the course. I have gotten the following answers: ab*, ababa, and a DFA recognizing aaaa (that I was tempted to give credit to but did not). Incidentally, the most common right answer has always been abab. Second is abba. PRO: I have this one early in the exam to calm them down.
I try to ask some of each type on an exam. However, sometimes a question can be easier or harder than you intended, or be harder to grade then you thought, or not be in category you thought it would be in. The hardest line to draw is which questions are a matter of mastery and which are a matter of creativity? Another issue- some students can abstract better than others.
When teaching a large course such as Sophomore discrete math (150-200 students) I tend to get a uniform distribution skewed a bit on the high side. More precise: I tend to get at roughly 10 students in EVERY 10-point interval: 0-10, 10-20, 20-30,..., 90-100, with less on the low side and more on the high side. The benefit of this is that the students who get (say) less than 40 CANNOT say Well--- everyone did badly. They really are send a signal to either work harder or drop (I tell them this directly as well). I don't understand profs who give exams where nobody cracks 50/100 (I have heard this is common in Physics). They are wasting half of the grade spectrum.
Published on September 03, 2013 07:54
August 28, 2013
The Dream
I have this theory that everybody's notion of "recent history" starts not from their memories but from their birth date. Case in point: Billy Joel's We Didn't Start the Fire. The first major event of my then very young life came from an oppressed people making their voices heard. The newspapers in the early days of my life were full of fear of violence that might come from the upcoming march on Washington. But 200,000 souls came out fifty years ago today in a peaceful demonstration asking for the basic freedoms the rest of America had.
Having moved to the birthplace of Martin Luther King, Jr from the hometown of the first black president, I know much has improved in the last fifty years. But we know King's dream is far from fulfilled, obvious to us from the paucity of African-Americans in our conferences and classes.
Take a moment of your day, watch the greatest speech of the 20th century, and remember how far America has come, and how far America has yet to go.
Having moved to the birthplace of Martin Luther King, Jr from the hometown of the first black president, I know much has improved in the last fifty years. But we know King's dream is far from fulfilled, obvious to us from the paucity of African-Americans in our conferences and classes.
Take a moment of your day, watch the greatest speech of the 20th century, and remember how far America has come, and how far America has yet to go.
Published on August 28, 2013 05:09
August 26, 2013
What are Galois Games?
How are math concepts named?
After the people who was involved with it. Examples: The Cook-Levin Theorem, Goldbach Conjecture, Ehrenfeucht-Fraisse games,
Banach-Tarski Paradox.
A descriptive name:
Examples: Chromatic Number; Girth of a graph (length of longest cycle). This resembles the definition of Girth in English though I have only heard the word used in mathematics;
Duplicator-Spoiler games.
A name that conjures up a nice image. Examples: Dining Philosophers problem;
The Monty Hall Paradox (though future historians will think he was a great Probabilist).
Name may have very little connection to the concept. Example: The Pell equation.
I saw an article whose title was Greedy Galois Games. I wondered what this game could be. Do the players alternate picking polynomials and if the composition is solvable by radicals then (say) Player I wins.
Did Galois invent some game?
The first game I thought of might be interesting; however, the paper was not about that. Nor was it about some game Galois invented. So---what is a Galois game? Aside from being a mathematician what else is known about Galois:
He died in a duel!In the article Greedy Galois Games they study a DUEL between two BAD DUELISTS. The idea is that if both have prob of hitting p (and p is small) and they want to make it fair, first Alice shoots, then Bob shoots the min number of times so that the prob of Bob winning exceeds Alice's, then Alice shoots a number of times so that her prob of winning exceeds Bob's, etc. The paper ends up involving the Thue-Morse sequence.
They are NOT using the name Galois the way we use Banach in Banach-Tarski Paradox, nor the way we use Monty Hall in The Monty-Hall Paradox. The fact that Galois was a mathematician has nothing to do with the naming, except that the authors may be more aware of Galois as a famous duel-loser. They could have used Alexander Hamilton (who lost a Duel to Aaron Burr) and then called them Greedy Hamiltonian Games, in which case I would assume that the game involved
Hamiltonian cycles or Quaternions.
Published on August 26, 2013 05:27
August 22, 2013
P = NP and the Weather
In the Beautiful World, my science fiction chapter of The Golden Ticket where P = NP in a strong way, I predicted that we could predict weather accurately enough to know whether it will rain about a year into the future. Besides putting Novosibirsk on the wrong side of Moscow, my weather prediction prediction has drawn the most ire from my readers.
Here was my thinking: Weather forecasting comes down to modeling. Find a good model, use the current initial conditions and simulate the model. P = NP can help dramatically here by making what should be the hardest part, finding the right model, easy. P = NP would help create much better models and should lead to far more accurate and deep forecasts than before. A year ahead prediction of weather didn't seem out of the realm of possibility.
As my readers point out, one cannot put in all of the initial conditions which would involve too much data even if we could get it, and small random events, the so-called butterfly effect, could dramatically change the weather in even a short period of time. Dean Foster, a Penn statistician, wrote me a short piece giving an analogy to a game of pool over time changed by the gravity generated by a single proton.
So how far can you predict the weather if P = NP? A month? Of course we'll probably never find out since I doubt P and NP are the same. In retrospect I shouldn't have put in such an aggressive weather forecasting because it detracts from other great things that happen if P = NP such as curing cancer.
Here was my thinking: Weather forecasting comes down to modeling. Find a good model, use the current initial conditions and simulate the model. P = NP can help dramatically here by making what should be the hardest part, finding the right model, easy. P = NP would help create much better models and should lead to far more accurate and deep forecasts than before. A year ahead prediction of weather didn't seem out of the realm of possibility.
As my readers point out, one cannot put in all of the initial conditions which would involve too much data even if we could get it, and small random events, the so-called butterfly effect, could dramatically change the weather in even a short period of time. Dean Foster, a Penn statistician, wrote me a short piece giving an analogy to a game of pool over time changed by the gravity generated by a single proton.
So how far can you predict the weather if P = NP? A month? Of course we'll probably never find out since I doubt P and NP are the same. In retrospect I shouldn't have put in such an aggressive weather forecasting because it detracts from other great things that happen if P = NP such as curing cancer.
Published on August 22, 2013 05:13
August 19, 2013
When Lance was 10 years old..
In honor of Lance's 50th birthday I ask the following: When Lance was 10 years old which of the following were true?
(Disclosure- some of the below are from a birthday card.)
A REMOTE meant a secluded spot off the beaten path.
CABLE was something that supported a bridge.
A VIDEO GAME was trying to make out what fuzzy images were on a snowy black and white 10 inch TV screen.
A CELL PHONE was what you used to make one phone call from jail.
A CALCULATOR was the accountant who did your parents taxes.
AN AIRBAG was someone who talked too much.
DIGITAL COMPUTING was counting on your fingers.
HIGH SPEED ACCESS was an on-ramp to the freeway.
SURFING was something done on a board in the ocean.
A BIRTHDAY was something Lance looked forward to.
A MOUSE was something you didn't want in your house.
A SPAM ASSASSIN was someone who killed people by giving them poisoned spam.
A WEB was what spiders wove.
A BUG was what spiders ate.
AMAZON meant where some big rain forest is (smaller now).
GOOGLE was an obscure term used by some math folks for the number 10100.
BING had no meaning.
APPLE was either a fruit or the record company founded by the Beatles. (There really WAS a legal name-issue when Apple-the-computer-company got into music.)
It was impossible to have 10,000 friends.
There were only three Network channels and a few local ones.
Music was on Vinyl records.
You went to the bathroom during commercials.
Johnny Carson joked that couples had sex during commercials on his show. (Ask your grandparents who Johnny Carson was, what commercials are, and what sex was.)
People read books written on paper.
Computer Science was not available as a major at most schools.
When people said you sound like a broken record they actually knew what a broken record sounded like.
People really would DIAL a phone number.
People would have to actually stop at toll booths instead of using easy-pass.
Long running TV shows would have one (or at most two) Christmas episodes since there were no arcs, hence an episode could be inserted into any season at any time. Contrast: M*A*S*H in its 11 seasons and 256 episodes had TWO Christmas episodes, where as 30 ROCK its 7 seasons and 131 episodes had FOUR Christmas episodes. (This may be THE least important consequence of the new technology.)
There were bar room fights over trivia since you couldn't just look it up on Google. The Guinness Book of World Records was supposed to cut down on bar fights, but it didn't quite work.
People knew how to read maps and get a sense of where things were instead of relying on technology. That's why today the number of hikers who get lost has skyrocketed.
If MTV existed they would still be playing music videos. The question Why doesn't MTV show Music Video's anymore has been asked so often it is now Cliche. But the above video provides an answer.
Lance did not recognize the importance of NP-completeness. Then again, neither had the math community, the non-theory computer science community, and Probably parts of the theory community.
To find out what time it was you couldn't look at your cell phone, TV set, or Microwave. You had to go outside and look at your sundial.
TV shows may have pilot episodes, or may not, but they didn't bother with explaining everything. Thought experiment: If Mr. Ed was on today
they would explain how he could talk (A government experiment gone wrong? gone right?) rather then the ONE line by Mr. Ed in the first episode: Don't try (to understand why I can talk)--- its bigger than both of us.
We all watched a TV show the same night. Contrast- last month I watched Firefly. Bizarre result of this--- since people can't find people to talk about shows as much as the used do, there is now a show called TALKING BAD where people on the show TALK ABOUT Breaking Bad.
True story: On March 9, 1967 John Smith (not his real name) wanted to watch Star Trek (Episode: Devil in the Dark) but his parents wanted to take the family out for dinner. So he pretended to be sick so he could watch it- because, as he puts it, if I don't see it now I will NEVER GET TO SEE THE EPISODE, EVER!!!!!. Imagine a world without DVR, DVD, TIVO, On-Demand, Hulu. He doesn't have to imagine it. Our younger readers do.
I think SURFING, MOUSE, and SPAM really have changed primary meanings. FRIENDS may have also.
(Disclosure- some of the below are from a birthday card.)
A REMOTE meant a secluded spot off the beaten path.
CABLE was something that supported a bridge.
A VIDEO GAME was trying to make out what fuzzy images were on a snowy black and white 10 inch TV screen.
A CELL PHONE was what you used to make one phone call from jail.
A CALCULATOR was the accountant who did your parents taxes.
AN AIRBAG was someone who talked too much.
DIGITAL COMPUTING was counting on your fingers.
HIGH SPEED ACCESS was an on-ramp to the freeway.
SURFING was something done on a board in the ocean.
A BIRTHDAY was something Lance looked forward to.
A MOUSE was something you didn't want in your house.
A SPAM ASSASSIN was someone who killed people by giving them poisoned spam.
A WEB was what spiders wove.
A BUG was what spiders ate.
AMAZON meant where some big rain forest is (smaller now).
GOOGLE was an obscure term used by some math folks for the number 10100.
BING had no meaning.
APPLE was either a fruit or the record company founded by the Beatles. (There really WAS a legal name-issue when Apple-the-computer-company got into music.)
It was impossible to have 10,000 friends.
There were only three Network channels and a few local ones.
Music was on Vinyl records.
You went to the bathroom during commercials.
Johnny Carson joked that couples had sex during commercials on his show. (Ask your grandparents who Johnny Carson was, what commercials are, and what sex was.)
People read books written on paper.
Computer Science was not available as a major at most schools.
When people said you sound like a broken record they actually knew what a broken record sounded like.
People really would DIAL a phone number.
People would have to actually stop at toll booths instead of using easy-pass.
Long running TV shows would have one (or at most two) Christmas episodes since there were no arcs, hence an episode could be inserted into any season at any time. Contrast: M*A*S*H in its 11 seasons and 256 episodes had TWO Christmas episodes, where as 30 ROCK its 7 seasons and 131 episodes had FOUR Christmas episodes. (This may be THE least important consequence of the new technology.)
There were bar room fights over trivia since you couldn't just look it up on Google. The Guinness Book of World Records was supposed to cut down on bar fights, but it didn't quite work.
People knew how to read maps and get a sense of where things were instead of relying on technology. That's why today the number of hikers who get lost has skyrocketed.
If MTV existed they would still be playing music videos. The question Why doesn't MTV show Music Video's anymore has been asked so often it is now Cliche. But the above video provides an answer.
Lance did not recognize the importance of NP-completeness. Then again, neither had the math community, the non-theory computer science community, and Probably parts of the theory community.
To find out what time it was you couldn't look at your cell phone, TV set, or Microwave. You had to go outside and look at your sundial.
TV shows may have pilot episodes, or may not, but they didn't bother with explaining everything. Thought experiment: If Mr. Ed was on today
they would explain how he could talk (A government experiment gone wrong? gone right?) rather then the ONE line by Mr. Ed in the first episode: Don't try (to understand why I can talk)--- its bigger than both of us.
We all watched a TV show the same night. Contrast- last month I watched Firefly. Bizarre result of this--- since people can't find people to talk about shows as much as the used do, there is now a show called TALKING BAD where people on the show TALK ABOUT Breaking Bad.
True story: On March 9, 1967 John Smith (not his real name) wanted to watch Star Trek (Episode: Devil in the Dark) but his parents wanted to take the family out for dinner. So he pretended to be sick so he could watch it- because, as he puts it, if I don't see it now I will NEVER GET TO SEE THE EPISODE, EVER!!!!!. Imagine a world without DVR, DVD, TIVO, On-Demand, Hulu. He doesn't have to imagine it. Our younger readers do.
I think SURFING, MOUSE, and SPAM really have changed primary meanings. FRIENDS may have also.
Published on August 19, 2013 10:29
August 15, 2013
Flash Gordon
We watched the movie Ted last week but this post isn't about that movie. The movie has several references to the 1980 movie Flash Gordon including an extended cameo by Sam Jones who played Flash.
Flash Gordon and its soundtrack from Queen saved me senior year of high school--whenever I felt down I would listen to the album and run the movie through my head escaping reality for a little bit. These were the days before videos and CDs, now I've rewatched the movie several times on DVD.
Flash Gordon was not a great movie by any means but it resonated with me with its action sequences, great music and corny lines like "Flash, I love you, but we only have fourteen hours to save the Earth!". The stars of the movie Sam Jones and Melody Anderson were and still are relatively unknown but it had a great supporting cast.
Topol, best known as Tevye in Fiddler on the Roof, played a scientist who many mocked for his crazy (but true) ideas of what was happening in outer space. Basically the same character as when he played Galileo.
Timothy Dalton played Prince Barin and would go on to be James Bond and the Max von Sydow, who played chess against Death in The Seventh Seal, was the Ming the Merciless.
What does this all have to do with computational complexity? Absolutely nothing. But today I turn 50, it's my party and I'll post what I want to.
Flash Gordon and its soundtrack from Queen saved me senior year of high school--whenever I felt down I would listen to the album and run the movie through my head escaping reality for a little bit. These were the days before videos and CDs, now I've rewatched the movie several times on DVD.
Flash Gordon was not a great movie by any means but it resonated with me with its action sequences, great music and corny lines like "Flash, I love you, but we only have fourteen hours to save the Earth!". The stars of the movie Sam Jones and Melody Anderson were and still are relatively unknown but it had a great supporting cast.
Topol, best known as Tevye in Fiddler on the Roof, played a scientist who many mocked for his crazy (but true) ideas of what was happening in outer space. Basically the same character as when he played Galileo.
Timothy Dalton played Prince Barin and would go on to be James Bond and the Max von Sydow, who played chess against Death in The Seventh Seal, was the Ming the Merciless.
What does this all have to do with computational complexity? Absolutely nothing. But today I turn 50, it's my party and I'll post what I want to.
Published on August 15, 2013 05:06
August 12, 2013
How much Trig does your governor know?
How much math should our public officials know? Basic probability and statistics so they can follow the arguments that their science advisers give them. And they should hire good objective science advisers and listen to them.
How much Trigonometry should a Governor know? Should a Governor know the angles of a 3-4-5 triangle? The following true story is paraphrased from Somewhat more than Governors need to know about Trigonometry by Skip Garibaldi.
The paper then proves the following:
When politicians say things that contradict current science (e.g., on evolution or global warming) I wonder if they know the truth and are lying to please their voters, or if they honestly don't know the truth.I also wonder which one is worse. In the case above I think Jeb honestly didn't know, and that's fine.
How much Trigonometry should a Governor know? Should a Governor know the angles of a 3-4-5 triangle? The following true story is paraphrased from Somewhat more than Governors need to know about Trigonometry by Skip Garibaldi.
In June 2004 Governor Jeb Bush of Florida was giving a talk to promote state-wide annual testing of students in public schools. A high school student asked him What are the angles in a 3-4-5 triangle? He responded I don't know. 125, 90, and whatever is left to add up to 180. Note that (1) he knew that 3-4-5 triangle has a 90 degree angle, (2) he knew that the angles of a triangle add up to 180, but (3) he didn't realize that 125+90 > 180. Still, I suspect most governors would do worse. The real answer is 90, 53.1 (approx), 36.9 (approx). A retired math professor was later quoted as saying I would not expect many mathematicians to know that.
The paper then proves the following:
The Governors Theorem: If a right triangle has integer
side lengths then the acute angles are irrational when measured
in degrees.
When politicians say things that contradict current science (e.g., on evolution or global warming) I wonder if they know the truth and are lying to please their voters, or if they honestly don't know the truth.I also wonder which one is worse. In the case above I think Jeb honestly didn't know, and that's fine.
Published on August 12, 2013 06:17
August 9, 2013
Don't Have an End Game
As a young professor, I wrote a grant proposal and took it to a senior theory professor for comments. He told me to take out the line "The ultimate goal of computational complexity is to settle the P versus NP problem." He agreed with the line, he just said that if we make these claims to the NSF then what happens after someone proves P different from NP? Nothing left to fund in complexity.
There was precedence here. In the 70s and 80s algebraists had the great goal of classifying all the finite simple groups. Once they were done, then what? Other examples are sending a man to the moon in the 60's or having a computer that beats the best human chess player.
Having an ultimate goal can be very motivating but quite limiting if that goal is actually reached. Luckily for us the P versus NP problem is a goal which will not likely be reached for a very long time.
There was precedence here. In the 70s and 80s algebraists had the great goal of classifying all the finite simple groups. Once they were done, then what? Other examples are sending a man to the moon in the 60's or having a computer that beats the best human chess player.
Having an ultimate goal can be very motivating but quite limiting if that goal is actually reached. Luckily for us the P versus NP problem is a goal which will not likely be reached for a very long time.
Published on August 09, 2013 06:52
Lance Fortnow's Blog
- Lance Fortnow's profile
- 4 followers
Lance Fortnow isn't a Goodreads Author
(yet),
but they
do have a blog,
so here are some recent posts imported from
their feed.



