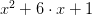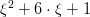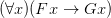Peter Smith's Blog, page 70

A Christmas card

Rogier van der Weyden, St Columba Altarpiece, c. 1455

With every good wish for a happy Christmas and a peaceful New Year.

The post A Christmas card appeared first on Logic Matters.

LaTeX for Logicians updated

Setting aside the other logic-related things I really ought to be doing, I’ve just been going in for a bit of constructive procrastination, systematically checking through the LaTeX for Logicians pages for the first time in almost three years. There’s some very minor re-arrangement, some renewing of broken links, and just a few new links.

As I’ve said before, whatever one’s issues and reservations about LaTeX for more general use, it is still surely quite invaluable for logicians. The LaTeX for Logicians pages continue to be heavily visited; so do please let me know how these pages can be improved, what new LaTeX packages of use to logicians that I have missed, etc.

The post LaTeX for Logicians updated appeared first on Logic Matters.

Postcard from the Bahamas

Bahamian evening

It’s a long flight, and not the most comfortable (thanks, BA). But lovely to be in the Bahamas again, on a family visit. Brexit news inescapable but all seeming particularly mad from this distance. Time for a lot of reading. I’ve particularly enjoyed Jonathan Raban’s Coasting (again!), Jill Paton Walsh’s A Desert in Bohemia  and am devouring Sally Rooney’s rightly much praised Normal People. Time too for re-thinking the dratted intro logic book: another month, another conception emerges of how best to organize things — but I hope there is at last convergence on a satisfying solution rather than just a continuing random walk though the options!

The post Postcard from the Bahamas appeared first on Logic Matters.

Tim Button, Loving the Universe

I was having coffee this morning with Thomas Forster, and we were talking — as you do — about theories with a universal set, and the claim that (a version of) Church’s Theory with a universal set is in fact synonymous with ZF. Doing a bit of googling around after our chat, I find that Tim Button has recently given a characteristically clear and lively talk about very closely related ideas, including developing some of Thomas’s. Here it is.

The post Tim Button, Loving the Universe appeared first on Logic Matters.

Six concerts, and a few CDs

The Chiaroscuro Quartet

For a small city, there is an extraordinary amount of music-making going on here in Cambridge  — there are many days during term when you can choose from half-a-dozen or more concerts, often of quite stellar quality.  And if you have the great good fortune to live near the centre, as we do, everything is all within easy walking distance too.

In the last few weeks, then, I have been able to hear Mitsuko Uchida play Schubert (though I find her playing has now become more than a little mannered and occasionally excessive in dramatic emphasis), and hear Angela Hewitt play Bach (the second book of the 48, which made for a very demanding evening! — though the wonderful control, the way Hewitt is able to bring out the fugal structures, combined with the emotional range she found from joyful to sombre contemplation, were all terrific). Then was a delightful concert from the Academy of Ancient Music and the BBC Singers of excerpts from Rameau and Lully operas — sheer enjoyment. Which isn’t ever quite the word to apply to a performance of Winterreise, but the prize-winning young baritone Samuel Hasselhorn was impressive and moving (I wasn’t so taken though with the playing of his accompanist on this occasion, the well-established Malcolm Martineau).

Then there were two quartet recitals I had been much looking forward to. The Jerusalem Quartet, however, I found distinctly disappointing. To be sure, their performances (Mozart ‘Hunt’, Beethoven ‘Harp’, Schubert Quintet with Gary Hoffman) were polished — well-engineered as it were. But even though it was the best possible setting, the very intimate space of the Peterhouse Theatre, I just couldn’t emotionally engage. The Takács started too in a rather disappointing way, with a routine-seeming Mozart K387 — though to be fair, this time I was at the back of a largish church, and the setting was far from ideal. But for Shostakovich’s  Quartet No. 4 they were on fire (enlivened by their younger new second violinist?), playing now with drive and intensity and emotional depth. And after the interval, an equally driven Mendelssohn  Quartet No. 6.

As it happens, I’d just been listening to a recommendable new CD of Mendelssohn quartets, from the Doric Quartet (whom I much admire) which also includes a performance of the sixth quartet — though the Elias Quartet or Quatuor Ébène perhaps  bring out the drama more. And talking of Quatuor Ébène, I’ve very much enjoyed this disc which I’ve only just disovered on iTunes, of the quartet playing with Manahem Pressler, as a 90th birthday celebration.

But the stand-out recent CD really has to be the wonderful Chiaroscuro Quartet playing Schubert. As a visceral experience, their Death and the Maiden — though transformed by the different sound world of their gut strings — is up there with the Pavel Haas Quartet’s award-winning recording. Extraordinary.

The post Six concerts, and a few CDs appeared first on Logic Matters.

Getting Things Right

I used to much enjoy contributing to the admirable Ask Philosophers site (you can check out my efforts here!) Rather sadly I had to give that up. But it seems that I can’t resist the pedagogic imperative. So my energies got  diverted instead to another  admirable question-and-answer site,  math.stackexchange; I occasionally do my bit there, when the spirit moves, to answer some elementary logic questions, trying to  Get Things Right.

A lot of my answers are to questions of no lasting interest. But  I’ve linked to an assorted 140 answers which are of perhaps more than ephemeral interest. There should be something here to amuse, even instruct, students at various levels.

Is contributing to a question-and-answer site like that worth doing? Well, there are far worse ways of procrastinating on the internet! But anyway, I’ve just noticed the estimate for the number of readers for my answers. And while we all know that idle browsing doesn’t in general mean that we are paying much attention, someone is unlikely to be visiting math.se and clicking on the link to an answer without some level of interest. I hope. Anyway, the stats are that approximately one million people have now viewed my answers there. Heavens!

Does that count as “impact”? Who cares! It is enough encouragement to continue. (But excuse me, must dash,  someone is wrong on the internet, confusing entailment and the material conditional yet again …!)

The post Getting Things Right appeared first on Logic Matters.

The Consistency of Arithmetic

There’s a nice new piece on the Consistency of Arithmetic by Timothy Chow in the Mathematical Intelligencer, which the author has made freely available. As he says in a FOM posting, he has put extra effort  into trying to make Gentzen’s proof accessible to the “mathematician in the street”. Of course, this kind of expository effort will always strike some readers as requiring too much of them to follow, and strike other readers as not going far enough into the details they want. But it seems an admirable effort to me, that students in particular could find pretty helpful.

The post The Consistency of Arithmetic appeared first on Logic Matters.

What Frege didn’t say about functions and quantification

Suppose you read this exposition:

Frege’s conception of a function is closely related to his discovery that quantifiers like (“for all”) and (“for some”) operate on what are now called open expressions — expressions containing free variables.

Say we’re interested in a series of calculations like this:

(A) and  and .

We soon begin to realize a pattern here; we are taking the square of a number, adding that to the result of multiplying the number by 6, and then adding 1. Following mathematical practice, we depict the pattern by replacing ‘3’ in first example in (A) by ‘x’:

(B)

This example pictures a function. Contemporary logicians think of such examples as having a variable reference; when the variable ‘x’ is assigned a number, this will refer to the result of applying the function to that number. Frege thought of (B) as having an indefinite reference. It corresponds to a function, which is something incomplete or unsaturated. Saturation is accomplished, and reference — say, reference to the number 28 — is achieved when a referring expression like ‘3’ is substituted for ‘x’  in (B).

You wouldn’t, I hope, be particularly happy about this as an account of Frege’s thought from a student. Leave aside the fact that dots aren’t yet joined up (to tell us how, for Frege, quantifiers do apply to expressions for functions mapping to truth-values). For a start, you’d want to point out that what express functions for Frege are expressions with gaps not expressions with free variables. So, for example, rather than (B) he would use

(C)

where the Greek letter is very clearly explained as a gap-marker, indicating that the two gaps are to be filled in the same way; and the Greek letters do not strictly belong to the concept-script, but are a convenient device in our metalinguistic commentary. And of course, Frege didn’t think that the likes of the gappy (C) as having indefinite reference. They have a definite reference to a function!

Now, it is true that — as well as the Gothic letters he uses as bound variables in his concept script, and the informal Greek gap markers  — Frege also uses italic Roman variables in his concept script. But Frege wouldn’t use them in an expression for a function comparable to (C) — for they are only to appear in expressions for assertible contents that can follow a judgement stroke.

Moreover, Frege’s Roman letters never occur in the scope of a corresponding explicit quantifier (in fact, they approximately function like parametric letters in natural deduction). For Frege, what quantifier expressions are applied to is — of course — open expressions in the sense of expressions with gaps, not to sentences with free variables. And — in modernized notation — we should think of the Fregean quantifier expression in e.g.

(D)

not as simply ‘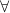’  nor as ‘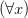’ (neither does any gap filling!) but rather as something we might represent as ‘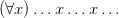’  which is applied to the gappy ‘’.

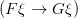And so it goes. It is a bit depressing, then, to report that the quotation above is lifted with only minor (and irrelevant) changes and omissions from p. 23 of a newly published CUP book aimed at linguistics students, Philosophy of Language, by Zoltán Gendler Szabó and Richmond H. Thomason. OK, I if anyone should know how difficult it is to write introductory logical stuff without corrupting the youth! But there is surely a boundary to how rough and ready you are allowed to be, and by my lights the authors overstep it here, given it would have been pretty easy to have been significantly more accurate without confusing the reader. And this sort of thing must make you wonder how trustworthy the authors are as guides elsewhere …

The post What Frege didn’t say about functions and quantification appeared first on Logic Matters.

Pretty serious people …

Posted by Wigmore Hall on Thursday, November 8, 2018

The post Pretty serious people … appeared first on Logic Matters.

Forgetting Turgenev?

Isaiah Berlin writes so well in his Russian Thinkers about Ivan Turgenev. Yes, Turgenev is — there on the surface — “a writer of beautiful lyrical prose, … the elegiac poet of the last enchantments of decaying country houses and of their ineffective but irresistibly attractive inhabitants, the incomparable story-teller with a marvellous gift for describing nuances of mood and feeling, the poetry of nature and of love”. We can indeed love him for that. But there is so much more. It is not for nothing that Turgenev’s books were so controversial when they appeared and (at least for Russians) long remained so. Yes, as Berlin puts it, “unlike his great contemporaries, Tolstoy and Dostoevsky, he was not a preacher and did not wish to thunder at his generation.” But he was deeply engaged from the beginning “with the controversies, moral and political, social and personal, which divide the educated Russians of his day; in particular, the profound and bitter conflicts between Slavophil nationalists and admirers of the west, conservatives and liberals, liberals and radicals, moderates and fanatics, realists and visionaries, above all between old and young. He tried to stand aside and see the scene objectively. He did not always succeed. But because he was an acute and responsive observer, self-critical and self-effacing both as a man and as a writer, and, above all, because he was not anxious to bind his vision upon the reader, to preach, to convert, he proved a better prophet than the two self-centred, angry literary giants with whom he is usually compared, and discerned the birth of social issues which have grown world-wide since his day.” (For “Slavophil nationalists vs admirers of the west” read “English nostalgists vs those who hanker after an ideal of ‘Europe’”: the bitter conflicts are still with us!)

I wonder though how much Turgenev is read now, at least here in the England he visited a number of times and which used to much admire him. Is even the great Fathers and Sons still on people’s ‘must read’ lists (their real lists, I mean, recording live intentions!)?  Or has cultural amnesia set in here too?

Turgenev was born on November 9th, in 1818 (October 28th, old style). So it is his bicentenary today — an occasion which seems to be passing here almost entirely unremarked. But I for one will be raising a glass of wine in his memory, as I sit down to reread once more his so evocative, so sad, novella First Love (wonderfully translated, in itself a work of love, by Isaiah Berlin).

The post Forgetting Turgenev? appeared first on Logic Matters.