Peter Smith's Blog, page 125

Carnap and the Diagonalization Lemma

Let me boldly fly a kite: this may be quite wrong, but do help me out if so! Anyway …

Carnap is often credited with proving the Diagonalization Lemma in Logische Syntax der Sprache. But, I claim, this is actually false if we understand 'Diagonalization Lemma' in what I take to be the usual modern sense. Why so?

Well, in §35 Carnap notes the general recipe for taking a one-place predicate 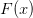and constructing a sentence 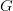such that 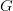is true if and only if 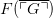is true, where as usual is  the formal numeral for the Gödel number for .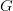

Fine. But that claim about constructing a semantic equivalence isn't the Diagonalization Lemma as normally understood, which is a syntactic thesis, not about truth-value equivalence but about provability. It is the claim that, in the setting of the right kind of theory 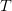, then for any one-place predicate 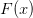we can construct a sentence 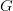such that 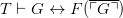. And Carnap doesn't prove that.

When we turn to §36, where Carnap proves the incompleteness of his system II, again he appeals to his semantic result not the syntactic Diagonalization Lemma. We now take the relevant predicate to be NOT-PROVABLE: so we get a sentence 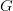which is true if and only if it isn't provable. And then Carnap appeals to the soundness of his system II to argue in the elementary way that 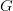isn't provable. So his is a version of the semantic incompleteness argument sketched in the opening section of Gödel 1931 (the one that appeals to a soundness assumption), and not a version of Gödel's official syntactic incompleteness argument which appeals to -consistency. Indeed, Carnap doesn't even mention -consistency in the §36 incompleteness proof. He doesn't need to.

Carnap doesn't use the theorem that his system II proves 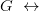NOT-PROVABLE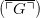, i.e. he doesn't appeal to an application of the Diagonalization Lemma in the modern sense. He doesn't need it, and he doesn't prove it.

So it is at best misleading to credit Carnap with the Lemma (unless that is qualified with a clear explanation that what is meant is a semantic result, not the syntactic one people usually mean).

If that's off-beam, do explain why!

Amethe von Zeppelin (continued)

A generous correspondent (much better at this Googling malarky than I) writes: "Amethe Smeaton was the daughter of a colonial administrator (later a liberal MP) called Donald Smeaton. She was born in the late 1890s and was at Girton College during WW1 but left without graduating because of ill health. She corresponded briefly with Russell about Principia in 1917. She married a Scottish army officer called Ian McEwan in 1919: they had a son who served in the Scots Guards and who was killed in WW2. In 1924 she published in the Morning Post an adulatory account of an interview she had with Mussolini (apparently she spent time in Italy as a child and therefore spoke Italian.) Graf von Zeppelin was cited as co-respondent in her divorce in 1929: it was said that they had been "found living as Count and Countess von Zeppelin" at Mentone. She married the count in Cap Martin, France in August that year. (He had been a German army officer during WW1, then had travelled in the forests of Bolivia, publishing an account of his adventures in 1926. According to A J Ayer, he chased Otto Neurath through the streets of Munich with a revolver at one point.) They bought a house called Schloss Mauerbach near Vienna in 1939. I think she died around 1966."

Amethe von Zeppelin

I've had Carnap's The Logical Syntax of Language on my shelves for over forty years. I can't say it was ever much consulted; but I've been reading large chunks of it today, in connection with Gödel. Carnap's book is often credited with the first statement of the general Diagonalization Lemma, and I wanted to double check this. (The credit seems to be somewhat misplaced in fact, but that's for my next post!)

Reading the early pages of the book, I've been struck by how good the 1937 translation seems. Well, I can't vouch for its accuracy — for I don't have the German to check — but it's very readable, and seems entirely sure-footed with the logical ideas. The translation is by Amethe Smeaton, who is warmly thanked in the Preface to the English Edition. But who was she?

A Countess von Zeppelin, no less. (But no, not the Countess who later threatened to sue Led Zeppelin for illegal use of her family name.) Which makes me wonder: what led the Countess to becoming a translator, and why did she become involved in this project. What was her background that made her an apt choice for translating this book of all books?

She'd translated before, a history book by Paul Frischauer, Prince Eugene: A Man and a Hundred Years of History, first published in German in 1933, translated in 1934, and still in print. Later she translated Schlick's Philosophy of Nature (1949), Walter Schubart's Russia and Western Man (1950), Bruno Freytag's Philosophical Problems of Mathematics (1951), and a book by Karl Kobald Springs of Immortal Sound (1950), on places in Austria associated with composers. She also co-translated Werner Heisenberg's Nuclear Physics (1953). That's a rather remarkable catalogue! And she wasn't "just" a translator: she was respected enough to be asked to review a group of logic and philosophy of science books for Nature in 1938 (she writes the composite review in a way that indicates she was very much up with developments).

But that is all I've been able to discover. Amethe von Zeppelin (that seems the name she most used) was, at least for a period, unusually knowledgeable about the then contemporary developments in logic and the philosophy of science, and it seems she had very wide intellectual interests (if we can assume a Countess von Zeppelin could at least choose which translations she wanted to take on). I'd like to know more. But, as Mrs Logic Matters opined, it seems she is another woman whose history has been written in water. Or is there someone out there who can help fill in her picture a little?

Somewhat gappy Gödel

When planning and actually writing my Introduction to Gödel's Theorems, I intentionally consulted other books as little as possible, trying to reconstruct strategies and proofs from memory as far as I could. I thought that would be a good discipline, and rethinking things through for myself would help me to explain things as clearly as possible. Well, people have indeed said nice things about the clarity of the resulting book, though my writing policy did mean I made a few nasty mistakes, some caught by pre-publication readers, and others corrected in later printings. I blush to recall ...

Anyway, now that I am working on a second edition, I want to spend the next month pausing to have a look at how others have handled the First Incompleteness Theorem. The basic shape of my book is fixed (after all, I'm doing another edition of IGT, not writing another different book, fun though that would be to do): but I might well get inspiration for how to make local improvements. So how do others state the Theorem? And how do they prove it? I'm planning to write up notes on expository themes and variations as I go along, and will post them here in due course.

The natural place to start is with Hilbert and Bernays. Slight problem: I don't have German (yep, schoolboy Greek was all well and good, but hasn't exactly been useful). Does anyone out there have detailed notes of how they prove the First Theorem in §5.1 of their second volume? I'd be really delighted to hear if so! Otherwise, there is a French translation, so I suppose I ought to do battle with that. Not that my French is any good these days either …

Until I can get hold of a translation of Hilbert and Bernays, then, the expository tradition for me will really have to start with Kleene's wonderful 1952 Introduction to Metamathematics. I'm looking forward a lot to dipping into that again. Then I counted over forty other books on my shelves which give more or less detailed proofs of the First Theorem: hours of fun ahead, obviously. But I've started, yesterday and today, by rereading Gödel's 1931 and his 1934 Princeton lectures. I have to blush again. I'd forgotten, for example, just what Gödel didn't prove in 1931. 'We shall only give an outline of the proof' that every recursive relation is (as we would now say) representable in P;  'the entire proof' [that for any predicate expressing a recursive property/relation there is an equivalent arithmetical predicate] 'can be formalized in the system P' [it can be, no doubt, but this isn't proved].

In fact, the situation is this. There are in fact two significantly different results stated in the 1931 paper, the 'semantic' and the 'syntactic' incompleteness theorems. The first requires that we are dealing with a theory which can express primitive recursive relations and is sound; the second version beefs up the first assumption and requires a theory which can represent p.r. relations while weakening the second assumption to require only that the theory satisfies the syntactic condition of omega-consistency. The first, 'semantic' theorem is sketched in Gödel's §1, the official 'syntactic' version is the topic of the central §2 and §3. Look carefully, however, and while there is (enough material for) a full proof of the underplayed semantic version, the proof of the 'syntactic' result (the result that is normally meant when people talk now about the First Theorem) is in fact gappy, gappier than I'd really remembered.

Meanwhile, I see over 200 people have downloaded the draft of the first eight chapters of the second edition. Thanks to David Auerbach and Seamus Bradley for some amazingly speedy comments. Keep 'em coming folks!

IGT2 A first instalment of the second edition of my Gödel book!

As I've said before, CUP have agreed to publish a second edition of An Introduction to Gödel's Theorems. Camera-ready copy is due to be sent to them rather implausibly soon, by the end of July 2012, with publication six months or so later(?). I have a slightly larger page budget, but don't at the moment intend adding chapters covering much new material: the plan is to do what the current edition does, but do it better (and with some proofs that are currently only sketched filled out better, as the book has a larger mathematical readership than perhaps I was expecting). I also plan (at last!) to have a proper sequence of sets of exercises, but here on the web-site, as there isn't room even in an expanded book.

OK, here then is

A first instalment of revised chapters of IGT2: Chapters 1 to 8

(these replace the current Chs 1 to 7). I've actually rather enjoyed doing this, and am quite pleased with the results — in particular, I think I've much improved the too-compressed incompleteness argument in the old Ch. 5. But I'm simultaneously also a bit cheesed off to see how much those early chapters did need improving. It all just goes to show that when you've finished writing a book, you should really put it in a drawer for three years until you realize what you were really trying to say, and then re-write it. You can just see your research-driven university approving of that policy, eh?

All suggestions/corrections for these revised chapters will be most gratefully received. You can put them in the comments below, though it is probably better all round to email them (my email address is at the bottom of the "About Peter Smith" page). For copyright reasons, I won't be able to make all the revised chapters so freely available when I've done them: but anyone who emails comments will be put on a circulation list for future tranches of the new version.

A Christmas card

Sandro Botticelli, Mystical Navitivity (detail)

With all good wishes for a peaceful Christmas

Just to keep you occupied over the holidays …

… and to dent your bank balances, here are three more rather sizeable logic books.

First up, spotted in the CUP bookshop and snapped up, is the just-published Proofs and Computations by Helmut Schwichtenberg and Stanley S. Wainer. A mere 450 action-packed pages, this looks as if it should be an instant classic, a welcome filling of a gap in the literature on the interactions between proof theory and computability theory.
Arnie Koslow told me about Lloyd Humberstone's The Connectives which has been been out a couple of months and somehow I'd missed seeing. This one weighs in at some 1500 pages (which makes the price rather remarkably cheap). Again, on a quick browse it looks daunting but amazing.
Very differently, I spotted an announcement a couple of days ago by Michael Gabbay of the publication of the first instalment of a translation of Hilbert and Bernays (or rather a bilingual text, German and English on facing pages). This only gets to p. 44 of the German text (over fifty pages of the book reprint a long essay by Wilfried Sieg on Hilbert's proof theory). But this is remarkably cheap, and being German-less I certainly wish the project well. So I'll be sending off for a copy.

So there you are: how can you resist? (Any since those aren't going to delay us very long —  are they? — any suggestions for recent books on logic matters that I might have missed?)

Next up: Truth, Gödel, and other delights

OK: a review of Maddy's very engaging recent book (written with Luca Incurvati, which was fun to do) has gone off to Mind. And in the next day or two, I must also put together a review for Phil. Math. of the altogether less engaging Kurt Gödel and the Foundations of Mathematics, which I was rather grumpily posting about here a few weeks ago.

Time then to pause to draw breath for Christmas after a busy/distracting time. But then what's next, logically speaking?

Well, I plan to blog here in the new year about two more books that I've been asked to review together — Leon Horsten's The Tarskian Turn: Deflationism and Axiomatic Truth and Volker Halbach's Axiomatic Theories of Truth. Not that I claim any special expertise about their topic: but then both books are written for a reader like me — a philosopher/logician interested in theories of truth, who wants to get a handle on recent some formal developments (to which the respective authors have been notable contributors). Should be very interesting. And since both books have been out for few months, I hope some readers of the blog will be able to chip in helpfully in comments!

But mostly, it will have to be back to Gödel. At the moment, I'm re-writing the opening chapters of the book for the second edition, and I think very much improving them — about which I have mixed feelings! On the one hand, it's very good to feel the effort of doing a second edition is going to be worth while, but on the other hand, I'm a bit downcast to see how very far from ideal those chapters previously were. Sigh. Anyway, when I've got the first tranche of chapters more to my liking, I'll post them here for comments.

And I've one or two other plans too … So watch this space!

Maddy on mathematical depth

This is a very belated follow-up to an earlier post on Penelope Maddy's short but intriguing Defending the Axioms.

In my previous comments I was talking about Maddy's discussion of Thin Realism vs Arealism, and her claim that there in the end — for the Second Philosopher — there is nothing to choose between these positions (even though one line talks of mathematical truth and the other eschews the notion).  What we are supposed to take away from that is the rather large claim that the very notions of truth and existence are not as central to our account of mathematics as philosophers like to suppose.

The danger in downplaying ideas of truth and existence is, of course, that mathematics might come to be seen as a game without any objective anchoring at all. But surely there is something more to it than that. Maddy doesn't disagree. Rather, she suggests that it isn't ontology that underpins the objectivity of mathematics and provides a check on our practice (it is not 'a remote metaphysics that we access through some rational faculty'), but instead what does the anchoring are 'the entirely palpable facts of mathematical depth' (p. 137). So '[t]he objective 'something more' our set-theoretic methods track is the underlying contours of mathematical depth' (p. 82).

This, perhaps, is the key novel turn in Maddy's thought in this book. The obvious question it raises is whether the notion of mathematical depth is robust and settled enough really to carry the weight she now gives it. She avers that '[a] mathematician may blanch and stammer, unsure of himself, when confronted with questions of truth and existence, but on judgements of mathematical importance and depth he brims with conviction' (p. 117). Really? Do we in fact have a single, unified phenomenon here, and shared confident judgements about it? I wonder.

Maddy herself writes: 'A generous variety of expressions is typically used to pick out the phenomenon I'm after here: mathematical depth, mathematical fruitfulness, mathematical effectiveness, mathematical importance, mathematical productivity, and so on.' (p. 81) We might well pause to ask, though, whether there is one phenomenon with many names here, or in fact a family of phenomena. It becomes clear that for Maddy seeking depth/fruitfulness/productivity also goes with valuing richness or breadth in the mathematical world that emerges under the mathematicians' probings. But does it have to be like that?

In a not very remote country, Feffermania let's say (here I'm picking up some ideas that emerged talking to Luca Incurvati), most working mathematicians—the topologists, the algebraists, the combinatorialists and the like—carry on in very much the same way as here; it's just that the mathematicians with 'foundational' interests are a pretty austere lot, who are driven to try to make do with as little as they really need (after all, that too is a very recognizable mathematical goal). Mathematicians there still value making the unexpected connections we call 'deep', they distinguish important mathematical results from mere 'brilliancies', they explore fruitful new concepts, just like us. But when they turn to questions of 'foundations' they find it naturally compelling to seek minimal solutions, and look for just enough to suitably unify the rest of their practice, putting a very high premium on e.g. low-cost predicative regimentations. Overall, their mathematical culture keeps free invention remote from applicable maths on a somewhat tighter rein than here, and the old hands dismiss the baroquely extravagant set theories playfully dreamt up by their graduate students as unserious recreational games. Can't we rather easily imagine that mind-set being the locally default one? And yet their local Second Philosopher, surveying the scene without first-philosophical prejudices, reflecting on the mathematical methods deployed, may surely still see her local mathematical practice as being in intellectual good order by her lights. Why not?

Supposing that story makes sense so far (I'm certainly open to argument here, but I can't at the moment see what's wrong with it) let's imagine that Maddy and the Feffermanian Second Philosopher get to meet and compare notes. Will the latter be very impressed by the former's efforts to 'defend the axioms' and thereby lure her into the wilder reaches of Cantor's paradise? I really doubt it, at least if Maddy in the end has to rely on her appeal to mathematical depth. For her Feffermanian counterpart will riposte that her local mathematicians also value real depth (and fruitfulness when that is distinguished from profligacy): it is just that they also strongly value cleaving more tightly to what is really needed by way of rounding the mainstream mathematics they share with us. Who is to say which practice is 'right' or even the more mathematically compelling?

Musings such as these lead me to suspect that if there is objectivity to be had in settling on our set-theoretic axioms, it will arguably need to be rooted in something less malleable, less contestable than Maddy's frankly rather arm-waving appeals to 'depth'.

Which isn't to deny that may be some  depth to the phenomenon of mathematical depth: all credit to Maddy for inviting philosophers to think hard about its role in our mathematical practice. Still, I suspect she overdoes her confidence about what such reflections might deliver. But dissenting comments are most welcome!

 

Back to Grice …

Piled on my study floor — part of the detritus from clearing my faculty office — are some box files containing old lecture notes and the like. I'm going through, trashing some and scanning others for old times' sake. (By the way, I can warmly recommend PDFscanner to any Mac user).

In particular, there is a long series of notes, some hundreds of pages, from a philosophy of language course that I must have given in alternate years, back in Aberystwyth. The set is dated around 1980 and would have been bashed out on an old steam typewriter. Those were the days. Some of the notes now seem misguided, some seem oddly skew to what now seem the important issues (such are the changes in philosophical fashion). But some parts even after all this time seem to read quite well and might be useful to students: so I'll link a few excerpts — either in their raw form or spruced up a bit — to the 'For students' page. Here, for example, is some very introductory material on Grice's theory of meaning. Having read too many tripos examination answers recently claiming e.g. that Searle refutes Grice, these ground-clearing introductory explanations might still provide a useful antidote!