Adib Hasan's Blog, page 2
June 30, 2019
A Week of Poetry: Day 1
I love poetry. Did I ever tell you that? Not really.
I also enjoy world-building, philosophy, travelling to new places, but I never write about any of my experiences. I don’t write about myself much.
Twenty years later, when I’ll ask myself if I lived the life I dreamed for, I will need a definitive answer. The best way to do so would be to document all the interested things happen to me.
I’ll start with poetry. This week I’ll post some of my favorite poems. The first one would be Song of the...
May 27, 2019
An Online Algorithm to Check for Bipartite Graphs
A graph \(G(V, E)\) is called bipartite if its vertices can be divided into two groups \(X\) and \(Y\) such that every edge connects one vertex from \(X\) and one vertex from \(Y\). The graph drawn below is bipartite.
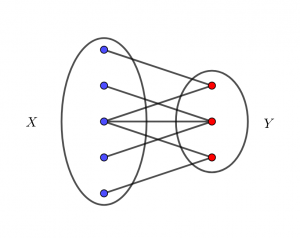
Given a graph, can you determine if it is bipartite?
This problem is pretty straightforward because the vertices of a bipartite graph can be colored with two colors such that every edge connects two vertices of different colors (see above). This property is cal...
May 19, 2019
How Game of Thrones Should Have Ended
This is a very unusual post for this blog. I hope my regular readers will bear with me.
I love Game of Thrones. I have read the books and the companion novels. I have been following the series for years. I am familiar with most of the fan theories too. Tonight the series finale aired. I didn’t like how the show ended. It felt rushed and very baffling.
I understand that I don’t get to question the showrunners’ creative decisions about the show. However, as a fan I can disagree with them. This...
April 14, 2019
A Blind Robot Beside an Infinite Wall
Let’s think about the following problem:
Consider a wall that stretches to infinitely in both directions. There is a robot at position \(0\) and a door at position \(p\in\mathbb Z\) along the wall \((p\neq 0)\). The robot would like to get to the door, but it knows neither \(p\), nor the direction to the door. Furthermore, the robot cannot sense or see the door unless it stands right next to it. Give a deterministic algorithm that minimizes the number of steps the robot needs to take to get t...
March 22, 2019
Prime Counting Function and Chebyshev Bounds
The distribution of primes plays a central role in number theory. The famous mathematician Gauss had conjectured that the number of primes between \(1\) and \(n\) is roughly \(n/\log n\). This estimation gets more and more accurate as \(n\to \infty\). We use \(\pi(n)\) to denote the number of primes between \(1\) and \(n\). So, mathematically, Gauss’s conjecture is equivalent to the claim
\[\lim_{n\to\infty}\frac{\pi(n)}{n/\log n}=1\]
This conjecture (currently known as the Prime Number Theor...
February 16, 2019
Multiplying Two Polynomials with Fast Fourier Transform
Polynomial multiplication is one of the most important problems in mathematics and computer science. It can be formally defined as follows: You are given two polynomials roughly of equal size,\[A(x)=a_0+a_1x+\dots+a_{n-1}x^{n-1}\]\[B(x)=b_0+b_1x+\dots+b_{n-1}x^{n-1}\]find a polynomial \[C(x)=c_0+c_1x+\dots+c_{2n-2}x^{2n-2}\] such that \(A(x)\cdot B(x)=C(x)\). At first, this may look like an easy problem, since you already know how to multiply polynomials. You … Continue reading Multiplying Tw...
February 10, 2019
No form of beauty
No form of beauty is as flawless, as abstract, or as perennial as the mathematical beauty that derives from unassailable logical perfectness, for a mathematical proof is not earthly science, but a poetry written in logic.
[ –Adib Hasan 
No form of beauty is as flawless, as abstract, or as pere...
No form of beauty is as flawless, as abstract, or as perennial as the mathematical beauty that derives from unassailable logical perfectness, for a mathematical proof is not earthly science, but a poetry written in logic. [ –Adib Hasan
February 2, 2019
Generating All Subsets of Size k in Python
Suppose you are given a set \(S\) with \(n\) elements and you need to generate every subset of size \(k\) from it. For instance, if \(S=\{3,4,5\}\) and \(k=2\), then the answer would be \(\{3,4\}\), \(\{3,5\}\), \(\{4,5\}\). So, how would you do that in Python? First of all, this is a really simple exercise. Stuff like … Continue reading Generating All Subsets of Size k in Python →
The post Generating All Subsets of Size k in Python appeared first on Reverberation.
January 29, 2019
Lie Detectors and the Story of Halting Turing Machines
Is it possible to design a machine that detects lies? Sure, people have already built devices called polygraphs that monitor blood pressure, respiration, pulse etc. to determine if a person is giving false information. However, that is not same as “detecting lies” because polygraphs merely measure physical effects of telling lies. On the top of … Continue reading Lie Detectors and the Story of Halting Turing Machines →
The post Lie Detectors and the Story of Halting Turing Machines appeared f...



